【EZR】逆数重み推定(IPW)でATT(被治療集団における処置効果)の推定手順【図解】

EZR

    この記事で学べること

      • 傾向スコアを用いた逆数重み推定法（IPW）とは？
      • ATT(被治療集団における処置効果)とは？
      • 重みづけをしたあとの背景情報のバランスの確認方法

    この記事のまとめ

      • 傾向スコアを用いた逆数重み法を使えばグループ間の背景が揃う
      • ただしどのような集団に着目した分析結果を得るかは重みの作り方によって異なる
      • EZRを使えば簡単に傾向スコアの計算とATT重みづけ推定ができる

    傾向スコアと逆数重み法とは

    傾向スコアとは

    傾向スコアについては，こちらの記事で解説しています．傾向スコアは平たく言えば「背景情報から予測される処置をうける確率」です．背景情報から計算される数値なので，背景情報をまとめたスコアとして考えることができます． 傾向スコアのように背景情報をまとめたスコアを利用する旨味は，一度に複数の背景の情報を扱うことができる点です．例えば処置をうけたグループ（処置群）と処置を受けなかったグループ（非処置群）がまったく背景の異なる集団だったら，フェアな比較はできません．ここでひとつひとつの背景情報を揃えるように組み合わせを考えると，膨大な作業コストがかかってしまいます．このときに沢山の背景情報をまとめたひとつのスコアを使うことができれば，その労力を払わなくて済むよね，ということです．

    傾向スコアを用いた逆数重み推定法（IPW）とは

    上記で説明した傾向スコアは一般的に，以下の方法で利用されます．

    • 多変量回帰モデルの共変量（説明変数のひとつとして）考慮する（ANCOVA）
    • 傾向スコアが近い処置群-非処置群でマッチングする（マッチング）※
    • 治療確率の逆数を使って水増しした疑似集団を作る（逆数重み法：IPW）

    本記事の話題は，最後の逆数重み法（IPW）についてです．IPWの詳しい説明やEZRを用いた実装方法はこちらの記事で紹介していますので，本記事だけで理解が難しければ，そちらも参考にしてみてください．簡単におさらいするとIPWでは，

    1. 処置群については処置を受ける確率の逆数（1/処置確率）で重みづけ
    2. 非処置群については処置を受けない確率の逆数（1/(1-処置確率)）で重みづけ

    することによって，もともとの集団を水増しした仮想的な集団を作り出します（疑似集団とよんだりします）．以下図のように，（１）処置群では赤色のひとたち，（２）非処置群では緑色のひとたちの分だけ，重みづけによって集団が水増しされています． 重みづけ前（左）には処置群と非処置群とに存在する対象者の特徴にはずれ（偏り）がありますが，上記で紹介した重みづけを行うことによって，同じような特徴をもった（同じような傾向スコアをもった）対象者が，処置群と非処置群で同程度存在するようになったことが分かります．これによって冒頭のフェアな比較が達成できそうです． ※本記事の本題ではありませんが，傾向スコアのマッチングについてはこちらの記事で解説していますので，興味があれば参考にしてみてください．

    全集団における効果（ATE）と被処置者における効果（ATT）の違い

    さて，ここからが本記事の本題です． 傾向スコアが1/3の女性（左から２列目）の女性は，重みづけ前（左）では両群あわせて３名存在しました．重みづけ後（右）では，処置群に３名，非処置群にも３名存在していて，それらを比べています．これは言い換えると，「傾向スコア1/3をもつ女性全員が処置を受けた場合と受けなかった場合を比較している」と言えます．実際にはそれぞれの対象者は，処置を受けている・受けていないのいずれかで，

    • 処置を受けた女性がもし処置を受けなかったら？
    • 処置を受けなかった女性が処置を受けていたら？

    という「もしも」は現実には観察できません．しかしIPWで疑似的に作り出した集団であれば，３名全員が処置を受けた場合と受けなかった場合を仮想的に作り出すことができているので，そのような「もしも」の効果の評価が理論上可能となります（これを「反実仮想」と呼びます）． ここからさらに話を「推定の対象（Estimand）」に伸ばしていきます．上記の傾向スコア1/3をもつ女性３名については，内１人が実際に処置を受けており，内２人が処置を受けていません．例えばあなたが医師だとして，自分が処方したお薬の効果をみたいとします．このときに「お薬の効果が知りたい」といっても色々なパターンがあり得ると思います．

    1. お薬を処方するかどうか悩みうる全ての患者さんにおける効果を知りたい（ATE）
    2. お薬を処方した患者さんにおける効果を知りたい（ATT）
    3. お薬を処方していない患者さんにおける効果を知りたい（ATU）

    １は上記の例で触れたように，３名の女性全員が処置をうける・うけない状況を仮想して比較するという状況です．最も一般的に行われるのはこちらの分析かもしれません．このような「集団全員における平均的な処置効果」をAverage Treatment Effect (ATE)と呼びます．以前に書いたこちらの記事で紹介しているIPWを用いた分析では，このATEを推定しています． ２については，お薬の処方を実際に受ける患者さんは他の患者さんとはやはり異なる特徴をもつひとたちで，相応の理由があったから治療を受けている可能性があります．この場合は治療を受けなかったような状態の患者さんたちの効果は関心の外であり，知りたいのは「実際に治療を受けた患者さんたちの効果」であると考えられます．つまり治療を受けた患者さんたちがもし治療を受けていなかったら？という場合と比較した効果を評価する必要があります．このような「処置を実際に受けた集団における平均的な処置効果」をAverage Treatment Effect on the Treated (ATT)と呼びます．臨床研究では本来重要なEstimandなのですが，日本の臨床研究の現場ではそもそもEstimandの考え方自体きちんと浸透していないので，分析においてATEと区別して利用されていないこともしばしばありそうです． ※PMDAとかはちゃんと区別するように喚起してますが現場教育の限界だと思います． ３については２の反対で，お薬の処方を受けなかった患者さんたちにもし処方していたら？を評価することになります．このような「処置を実際に受けなかった集団における平均的な処置効果」はAverage Treatment Effect on the Untreated (ATU) と呼ばれます． 今回の主題は「ATEではなくATTを推定する方法」なので，次節からは実際の手続きについて紹介します．

    被処置者における効果（ATT）推定のための重みづけ

    ATTを推定するときの目標は「処置を受けた集団がもし処置を受けていなかったら？」という仮想の集団を作り出すことです．当然，すでに処置を受けたひとたちからはそのような集団は作れません．従って処置を受けていない集団の分布を重みづけによって変化させることで，そのような仮想集団を作り出すことを目的とします． 以下の図は，重みづけを行う前のオリジナルな集団です．処置群と非処置群に属する人の特徴（＝傾向スコア）がずれていることが分かります．この特徴のずれがあると，群間でのフェアな比較が出来なくなって（バイアスが生じて）しまいます． ここでIPWを利用して，この背景のずれを小さくすることが今回の目的です．特に今回はATTを推定するため，処置群と同じような背景情報をもつ非処置群を作り出します．そのため基準となる処置群については，重みはつけません（つまり重みは１）．従って処置群の特性の分布は変わりません． 続いて非処置群の特性の分布を，処置群に類似した形になるように，以下の重みをつけます． 重み = 傾向スコア/(1-傾向スコア) 実はこの重みは，

    1. ATEと同様に 1/(1-傾向スコア) = 処置を受けない確率の逆数　で重みづけした後に，
    2. 傾向スコア＝処置を受ける確率　を掛けている

    と同様の手続きを踏んでいることになります．つまり一度（１）疑似的な全集団（ATEで考えた集団）を作り出してから（２）処置確率（集団内で処置を受けている）を掛けることで治療群と同じ分布に近づけるという手続きをふんでいます． ※実は処置群についても，ATEと同様に1/傾向スコアの重みづけをした後に傾向スコアを掛ければ，結果的に重みは１になるので，同じ手続きをふんでいると考えることが出来ますね． 具体的には以下のような計算を経ることで，薄い白色の方々が減り，緑の方が水増しされています． このような重みづけによって得られた特性の分布について，処置群間で並べてみます．以下の通り，極端な特性を持つ方以外は，非処置群の分布が処置群に近づいたことが分かります．これで重みづけ前よりも，フェアな比較が実現できそうです． 上記の手続きによって，処置群に近い特性をもつ疑似的な非処置群を作り出すことで「処置群がもし処置を受けていなかったら？」という反実仮想を考えることができます．これまでのATEとは異なり，処置を受けた集団に特異的な効果を推定しているため，この推定対象はATTと呼ばれるということです． 当然，傾向スコアの逆数重み法を利用しなくても，ATTは推定可能です．こちらの記事で紹介している傾向スコアマッチングも，治療をうけた対象者を基準としてマッチング相手を探しているため，実はATTに近いものを推定していると考えられるケースが殆どです．（もちろんマッチングにも色々な方法があり，その方法やデータの内容によって推定できている対象が異なることに注意してください．）

    EZRを利用した逆数重み法によるATT推定

    それでは早速データセットを利用して逆数重み法によるATTを推定してみましょう．

    データセットをダウンロードして読みこむ

    データセットは練習用のCSVデータを準備しましたので，手元にちょうどよいデータがなければ，これらをダウンロードしてご利用ください．

    id iv cnf1 cnf2 ・・・ outcome_num outcome_skew outcome_ord time
    1 0 0.14 0 ・・・ 200.9 0 1 0.04
    2 0 0.41 1 ・・・ 160.37 0 1 0.11
    3 1 -0.07 0 ・・・ 461.07 158.34 3 0.08
    4 1 -0.25 0 ・・・ 363.76 76.03 2 0.02
    5 0 0.7 0 ・・・ 290.58 0 1 0.02
    ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・
    496 0 -1.35 1 ・・・ 227.81 0 1 0.11
    497 0 1.03 0 ・・・ 170.44 0 1 0.17
    498 1 -0.81 0 ・・・ 326.61 44.92 2 0.2
    499 1 1.8 0 ・・・ 256.07 0 1 0.13
    500 0 1.77 0 ・・・ 197.09 0 1 0
    robustwife_all.csv ※11人目以降は省略

    準備１．参考データ（CSV）をダウンロード

    アイコン

    練習用CSVデータをダウンロード

    1 ファイル 42.61 KB
    ダウンロード

    ※後ほどEZRで読み込みたいデータの場所を指定する必要があるため，デスクトップなど自分が分かりやすい場所に保存しておくことをおすすめします！

    準備２．EZRを起動 ⇒ CSVファイルの読み込み

    CSV・ExcelファイルのEZRにおける読みこみ方は，以下で詳しく説明していますので，参考にしてみてください．今回はデータセット名はデフォルトのまま Dataset と名前をつけて読みこんでいます．

    https://robustwife.com/ezr-how-to-read-dataset/

    傾向スコア＆各群に所属する確率の逆数を計算する

    まずは傾向スコアを推定してみましょう．このステップは基本的に傾向スコアマッチングの記事で紹介した内容と同じものになります． 先ほどの復習になりますが，ATTを推定するときの手続きは，

    1. ATEと同様に 処置を受ける/処置を受けない確率の逆数（各群に属する確率の逆数）で重みづけ
    2. 傾向スコア＝処置を受ける確率　を掛ける

    なので，まずはATEの推定の時と同様に，傾向スコアをロジスティック回帰モデルで推定すると同時に，各群に所属する確率の逆数（重み）を計算します．

    今回は処置変数である treat_bin (1:処置あり, 0:処置なし) に関する傾向スコア（treat_bin=1となる予測確率）を背景情報である cnf1 と cnf2 から計算してみます．EZRの画面で，

    1. 名義変数の解析
    2. 二値変数に対する多変量解析（ロジスティック回帰）
    3. 目的変数 欄にカーソルをあてて処置変数 treat_bin をダブルクリック（※1）
    4. 説明変数 欄にカーソルをあてて交絡因子 cnf1 と cnf2 をそれぞれダブルクリック（※2）
    5. ☑傾向スコア変数を自動作成する にチェックを入れる
    6. ☑逆数重みづけ(IPW)のデータセットを作成する にチェックを入れる
    7. OK

                ※1．画面を開いた時点ですでに「目的変数」欄にカーソルが当たっているはずです ※2．treat_bin をダブルクリックしたら自動的に「説明変数」欄にカーソルが移動します

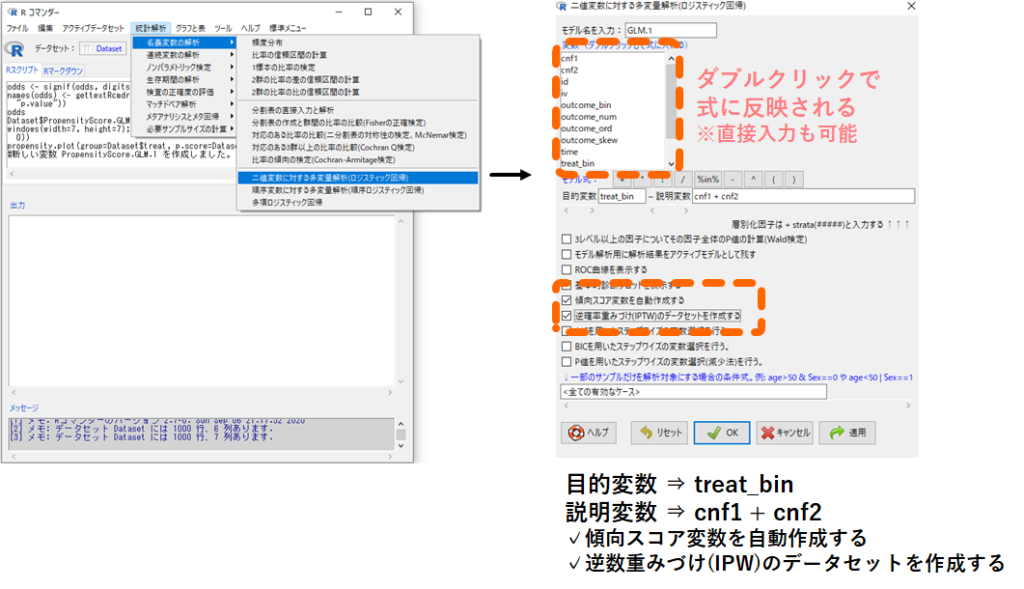
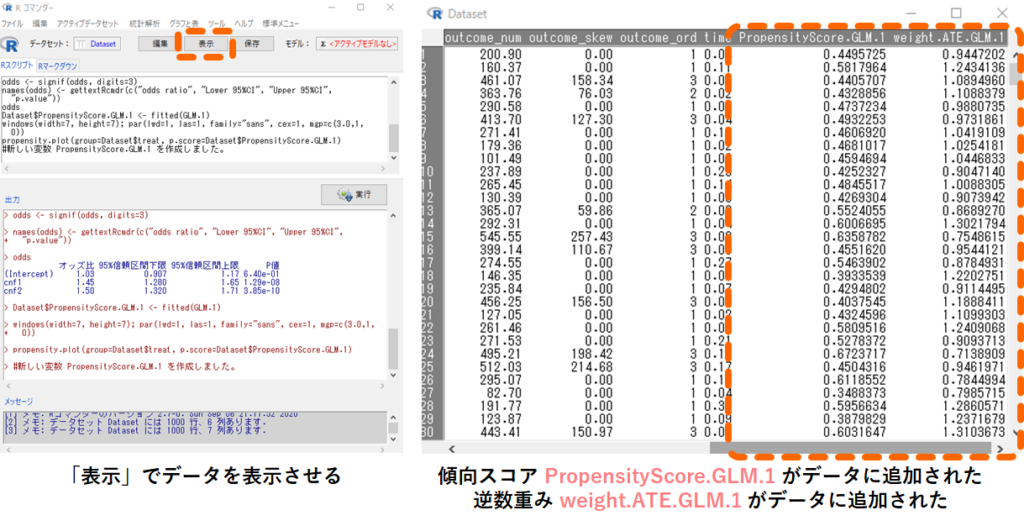
                これで各対象者について，背景情報 cnf1 と cnf2 から計算された傾向スコアと逆数重みがデータDatasetに保存されているはずです．早速データの中身を以下手順で見てみましょう．

                データの右端に「PropensityScore.GLM.1」という新しい変数ができていますね．これがcnf1とcnf2から予測した各研究対象者において処置が行われる確率であり，傾向スコアになります．

                また「weight.ATE.GLM.1」という新しい変数も同時に作成されています．これは各グループに所属する確率の逆数となりますので，今回逆数重み法で利用する重みになります．

                ATTを推定するための重みを計算する（各群に所属する確率の逆数×傾向スコア）

                ATT推定では，各群に所属する確率の逆数×傾向スコアが重みとなります．これはEZRで自動的に計算はされないので，データセットに編集を加える必要があります．データセットの編集は「アクティブデータセット」で行います．以下の手続きで，データセットに含まれる各群に所属する確率の逆数（weight.ATE.GLM.1）と傾向スコア（PropensityScore.GLM.1）を掛けた新しい重み変数を作成しましょう．

                1. アクティブデータセット
                2. 変数の操作
                3. 計算式を入力して新たな変数を作成する
                4. 新しい変数名に「weight.ATT」と入力する（任意の名前を指定できます）
                5. 計算式に「weight.ATE.GLM.1*PropensityScore.GLM.1」と入力する※
                6. OK

                ※現在の変数のリストに含まれる変数名をダブルクリックすると，計算式のカーソルが当たっている部分に変数名が代入されます．掛け算記号の*は自身で入力する必要があります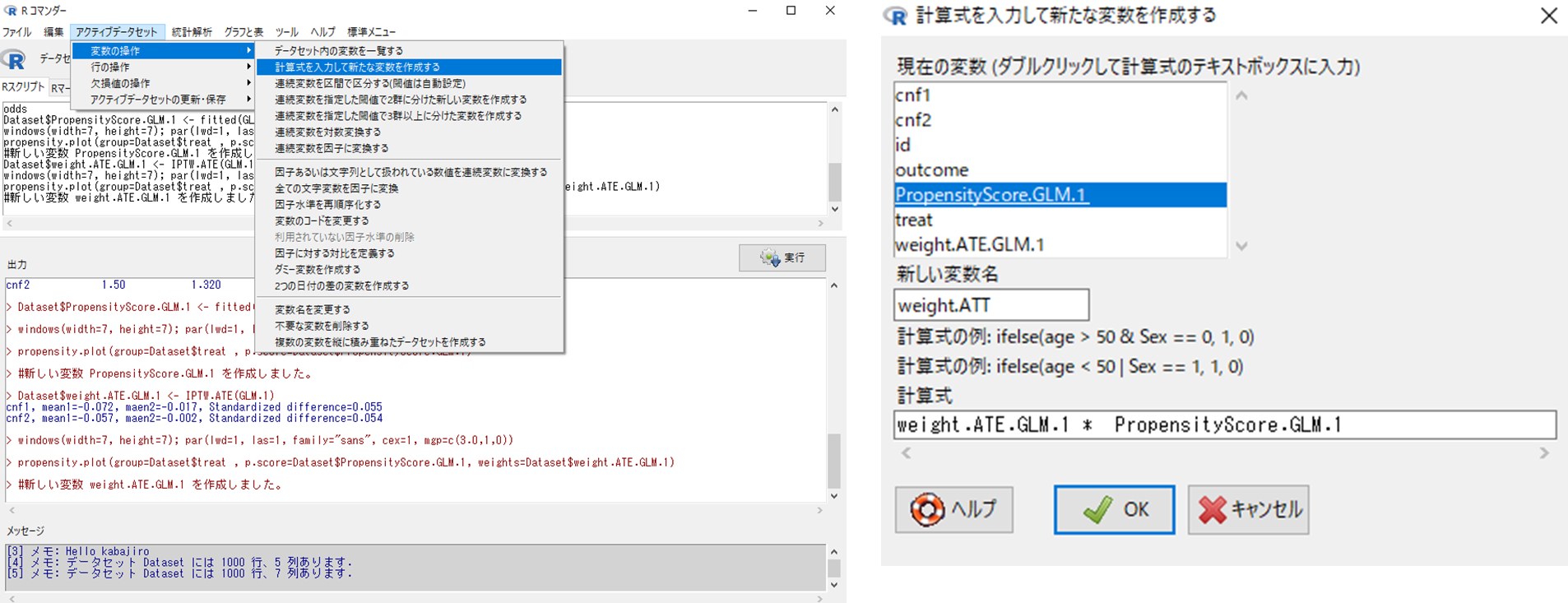． 上記の手続きで作成された weight.ATT 変数は，新しいカラムとしてデータセットの右端に追加されています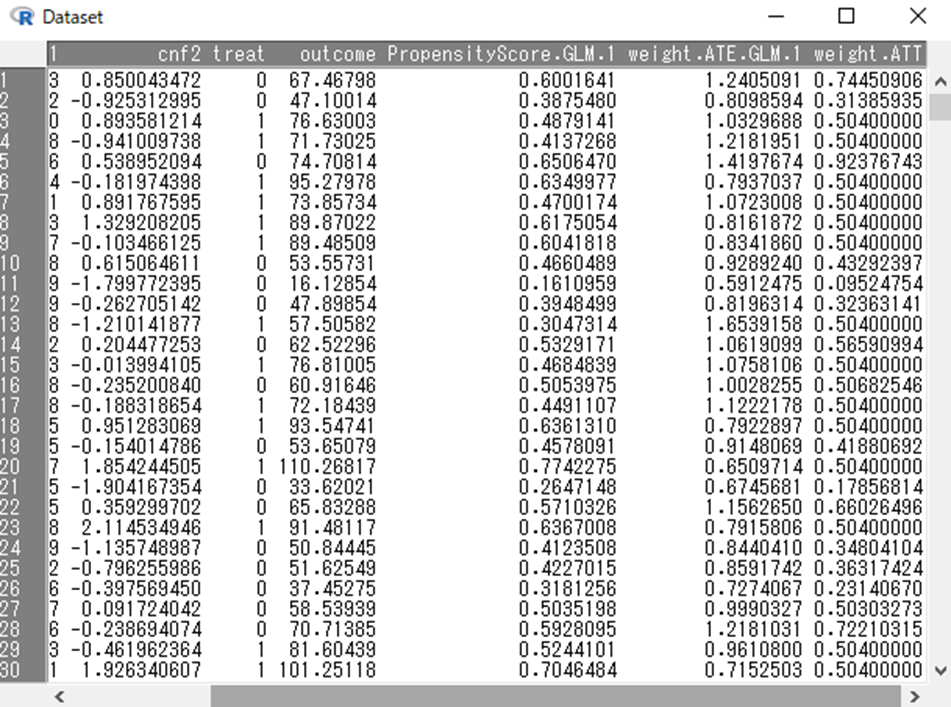． ここでお気づきの方がいらっしゃるかもしれません．ATTの重みなのに処置群（treat=1）の重みが１になっていない，すべて 0.504 になっていると．．．君のような勘のいいガk．．． 実はEZRで　☑逆数重みづけ(IPW)のデータセットを作成する　機能を利用すると，Stabilized weight（安定化された重み）というものが計算されるようになっています．といっても複雑なことではなく，ATEの重みに，

                • 治療群：集団全体における処置をうけた対象者の割合（今回のデータでは0.504）
                • 対照群：集団全体における処置をうけない対象者の割合（今回のデータでは1-0.504=0.496）

                を掛けているだけです※．これはこのような操作をすると，推定量の精度を向上させたりすることが出来るというメリットがあります．この辺りは以下の論文がとても参考になります． Robins, J., Hernán, M., & Brumback, B. (2000). Marginal structural models and causal inference in epidemiology. Epidemiology (Cambridge, Mass.), 11(5), 550–560. https://doi.org/10.1097/00001648-200009000-00011 Austin, P. C., & Stuart, E. A. (2015). Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Statistics in Medicine, 34(28), 3661–3679. https://doi.org/10.1002/sim.6607 ※イメージしずらいかもしれませんが，この操作をすると重みづけによって背景を揃えたまま，治療群は元々の治療群の人数に，対照群は元々の対照群の人数に再度圧縮することができます． 上記を考慮すると，全ての処置群の重み１には処置者の割合0.504がかけられているため，weight.ATTが0.504になっていることは納得できます．もしこの重みを１に戻したければ，当然処置者の割合0.504で割ってあげればOKです．当然，対照群についても同様に非処置者の割合0.496で割ってあげれば，ここまでで紹介してきた重みに戻ります． 但し上述のとおり，安定化された重みを利用することは多くのケースで推奨されることが多いため，weigth.ATTをそのまま利用して問題ありません．ここからはこの安定化されたweight.ATTを利用して話を進めます．

                重みづけ後の特性分布の比較＆ATTを推定する

                このステップについては，ATEをIPWで推定した手続きと全く同じなので，以下記事の「２．重み付け前後で背景情報のバランスを確認する」や「３．重み付けを考慮しながらグループ間の比較を行う」をご参照ください．

                【EZR】傾向スコアによる逆数重み推定(IPW)の解析手順【図解】
                傾向を用いた逆数重み推定法（IPW）をしてみたいけど，手順が分からなくて困っていませんか？ この記事ではEZRを利用したIPWのコンセプトや手順をなるべく丁寧に紹介しています． 実際の実行画面をもちいて図解していますので，初心者の方も安心して取り組めます． 早速EZRでのIPWを体験してみましょう！
                robustwife.com
                2021.04.10

                まとめ

                今回はEZRを用いた逆数重み推定法（IPW）によってATTを推定する一連の流れについて紹介しました．従来のATEを操作するIPWから一歩先に進んでいるため，少し難しく思えるかもしれませんが，個々が理解できれば因果推論がもっと身近に感じられると思います．

                EZR開発者の先生が出されている書籍や，因果推論についてもっと専門的なところまで勉強したいという方にお勧めの書籍も以下に紹介しておきます．

                コメント

                タイトルとURLをコピーしました