記事の要約:EZRで傾向スコアによる逆数重み推定(IPW)の解析手順【図解】
この記事で学べること
- EZRによる傾向スコアの計算方法
- 傾向スコアを用いた逆数重み推定法(IPW)とは?
- 傾向スコアを用いた逆数重み推定量の計算方法
- 重みづけをしたあとの背景情報のバランスの確認方法
この記事のまとめ
- 傾向スコアは背景情報から予測された処置をうける確率
- 傾向スコアを用いた逆数重み法を使えばグループ間の背景が揃う
- EZRを使えば簡単に傾向スコアの計算と重みづけ推定ができる
- EZRや因果推論に関する書籍は以下がおすすめ
- (因果推論をRで学びたい方向け)統計的因果推論の理論と実装 (Wonderful R)
- (因果推論をPythonで学びたい方向け)つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門
- (因果推論の理論も学びたい方向け)調査観察データの統計科学: 因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
傾向スコアとは
傾向スコアに関する基本的な説明はこちらの記事で解説しています.この記事でもざっくりと要点だけを復習しておきます.
- 比較するグループ間でもともとの背景が違うと比較結果は信頼できなくなる(交絡)
- グループ間の背景情報のバランスをとるために傾向スコアを用いた手法が利用できる
- 傾向スコアは「背景情報から予測される処置をうける確率」として計算できる
- 傾向スコアを用いて交絡を取り除く方法はマッチング・逆数重み法(IPW)などがある
つまりグループ間の比較をフェアにするのであれば,グループ間の状態を揃えてあげる必要があり,そのときに傾向スコアはとても便利だよ,ということです.
こちらの記事では傾向スコアを使ったマッチングの解析手順について説明していました.今回は良く使われる傾向スコアの利用方法2ということで,傾向スコアによる逆数重み推定法(IPW; Inverse Probability Weighted estimator)について紹介します.
傾向スコアを用いた逆数重み推定法(IPW)とは
傾向スコアを用いた逆数重み法とは,その名前の通り,各対象者のデータを傾向スコア(厳密には所属するグループに割り当てられた確率)の逆数で重みづけしてあげる方法です.重みづけするというのは「水増しする」というイメージをもってもらえば分かり易いかと思います.例えば重みが「2」であれば,その対象者のデータは2人ぶんとして考える,といったイメージです.
さて,それでは傾向スコアの逆数で重みづけるとはどういうことでしょうか?図でみてみましょう.まず,以下のように,より具合の悪い人が処置をうけているような例を考えてみます.このようなデータでは,もともとの状態がグループ間で異なるためにフェアな比較ができず,処置群に不利な結果がでてしまいますよね.
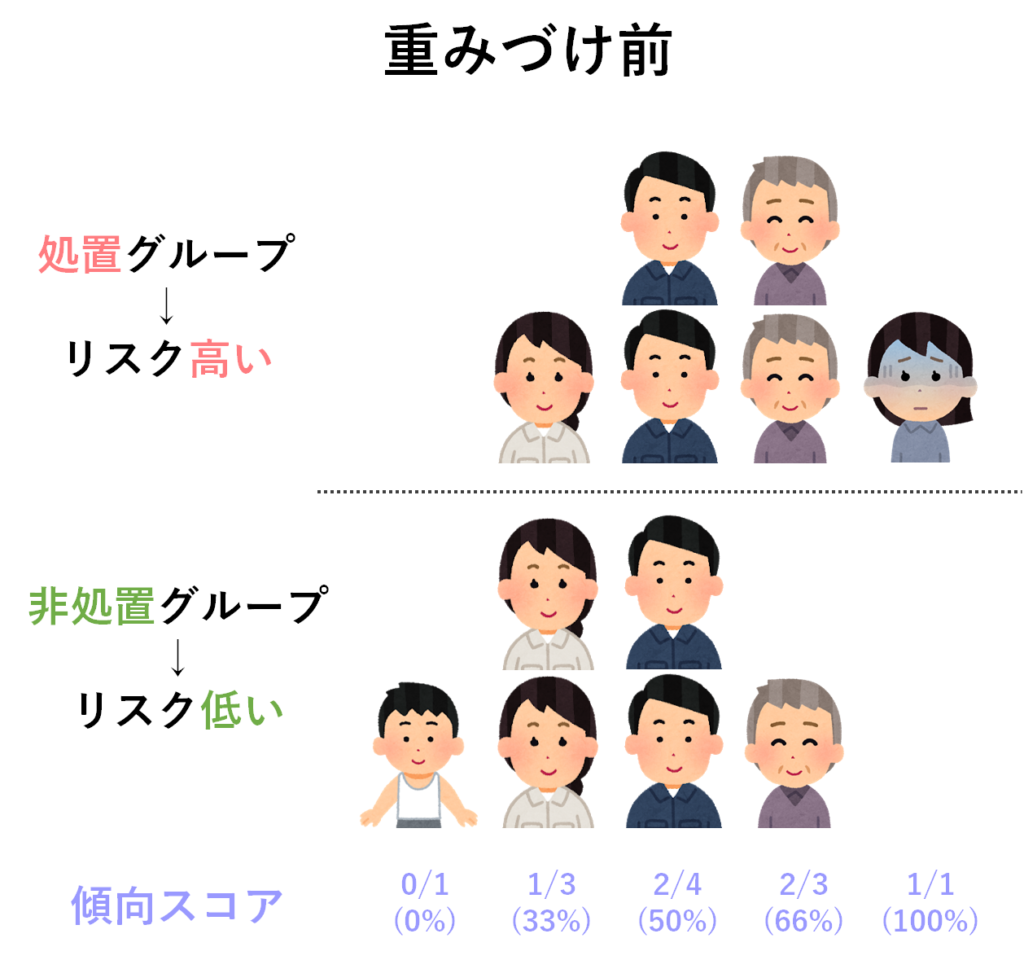
それでは傾向スコアを利用した逆数重みを適用してみましょう.基本的なルールとして,以下の操作を覚えておいて下さい.
- 処置群:処置をうけた確率の逆数(=傾向スコア の逆数)で重みづけ
- 非処置群:処置をうけなかった確率の逆数(=1-傾向スコア の逆数)で重みづけ
まずは「処置群」について考えます.処置群では,それぞれの対象者のもつ傾向スコアの逆数をかけた分だけ,人数を水増しします.例えば傾向スコアが1/3=33%の場合,その逆数は3/1なので,人数を3倍してあげればOKです.他の対象者についても同様に計算して,ここでは水増しした人数を赤色で表示しておきます.

次に非処置群について考えてみます.非処置群では「処置をうけない確率」の逆数で水増しします.処置をうけない確率は,1-傾向スコアで計算できます.例えば傾向スコアが1/3=33%の場合,1-1/3=2/3であるため,その逆数は3/2となります.従って人数を3/2倍してあげればOKです.他の対象者についても同様に計算して,ここでは水増しした人数を緑色で表示しておきます.
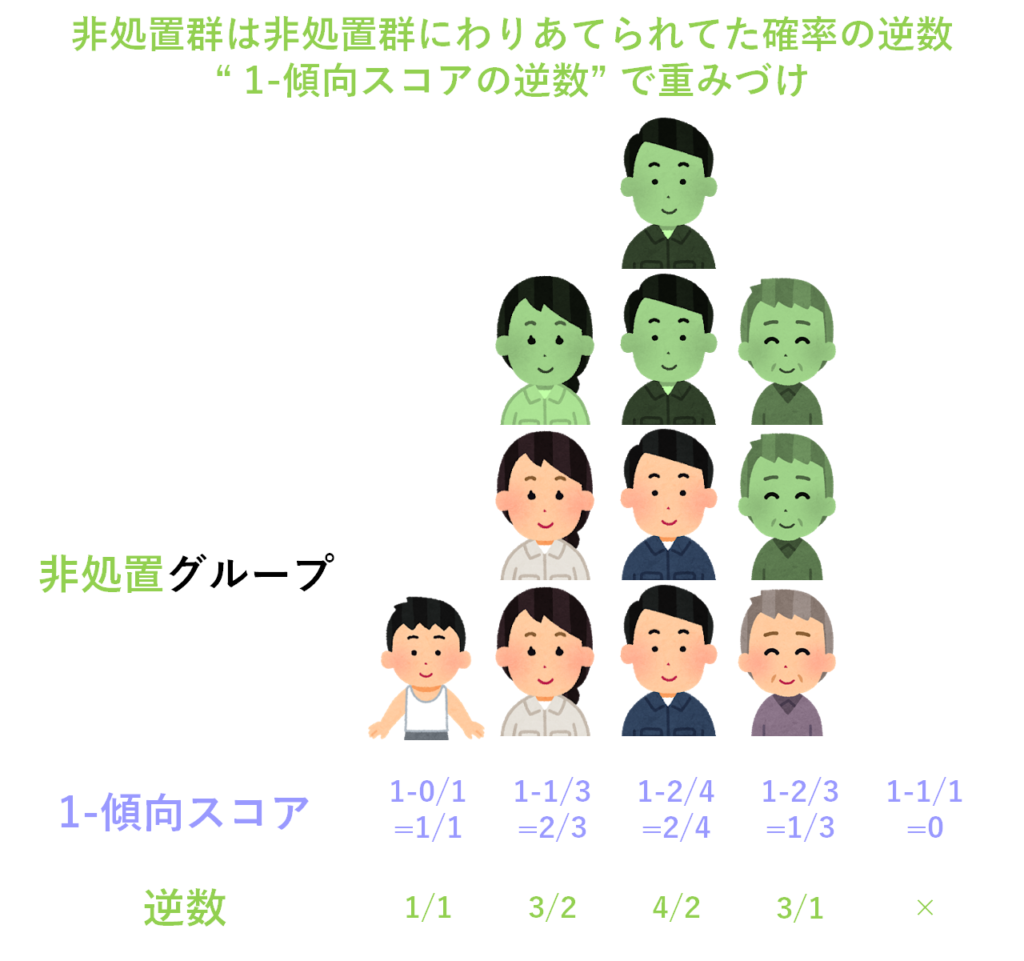
これで重みづけは完了です!重みづけ前後で,対象者の分布がどのように変わったか確認してみましょう.
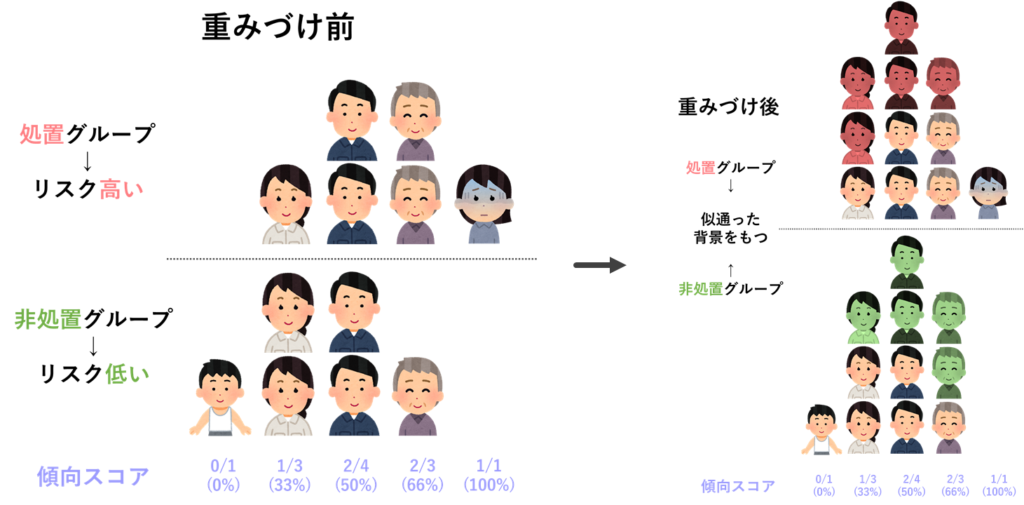
どうでしょうか?重みづけをした後は,両端の極端な傾向スコアをもつ対象者以外の人数は均等になりましたね!この状態であれば,重みづけ前の状態よりも,グループ間の比較をフェアに行うことができそうですね.
あとは両端の極端な傾向スコアをもつ対象者についてですが,これはもっと端的にいうと「相手のグループに類似した傾向スコアをもつ人がいない」対象者たちです.傾向スコアマッチングでは,マッチング相手が見つからず,マッチングデータに抽出されなかった人たちですね.この人たちの扱い方については種々方法がありますが,比較するグループ間で重ならない範囲の傾向スコアをもつ対象者は重みづけ前に解析から除外する,あるいは傾向スコアを5%や95%などの値に丸め込む等,この辺りも状況によって色々な手法が提案されています.今回も,そのような両端の対象者を切り捨てて解析を行えば,両グループ間の対象者の分布が一致することが分かりますね.
傾向スコアを利用した逆数重み法の重要なコンセプトは,ここまで理解できればまず大丈夫です.あとは,この重みづけした解析をどうおこなうかですが,ポイントが2つあります.
- グループ間の比較を重みづけして行う(実際にデータが水増しされるわけではない)
- 重みづけした推定量は標準誤差の推定に工夫が必要
この辺りの実際の解析の操作方法については,以下のEZRでの解析手順で説明していきます.ただEZRだけでは,重みの計算まではできても,実際にその重みを適用した解析自体は実行できません.そのためEZRのスクリプト画面に,Rのコードを追記する必要がありますので,ちょっと上級者向けになります.
事前準備:データのダウンロードと読み込み
それでは早速データセットを読みこんで解析していきましょう.
データセットは練習用のCSVデータを準備しましたので,手元にちょうどよいデータがなければ,これらをダウンロードしてご利用ください.
| id | iv | cnf1 | cnf2 | ・・・ | outcome_num | outcome_skew | outcome_ord | time |
| 1 | 0 | 0.14 | 0 | ・・・ | 200.9 | 0 | 1 | 0.04 |
| 2 | 0 | 0.41 | 1 | ・・・ | 160.37 | 0 | 1 | 0.11 |
| 3 | 1 | -0.07 | 0 | ・・・ | 461.07 | 158.34 | 3 | 0.08 |
| 4 | 1 | -0.25 | 0 | ・・・ | 363.76 | 76.03 | 2 | 0.02 |
| 5 | 0 | 0.7 | 0 | ・・・ | 290.58 | 0 | 1 | 0.02 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 496 | 0 | -1.35 | 1 | ・・・ | 227.81 | 0 | 1 | 0.11 |
| 497 | 0 | 1.03 | 0 | ・・・ | 170.44 | 0 | 1 | 0.17 |
| 498 | 1 | -0.81 | 0 | ・・・ | 326.61 | 44.92 | 2 | 0.2 |
| 499 | 1 | 1.8 | 0 | ・・・ | 256.07 | 0 | 1 | 0.13 |
| 500 | 0 | 1.77 | 0 | ・・・ | 197.09 | 0 | 1 | 0 |
※11人目以降は省略
準備1.参考データ(CSV)をダウンロード
※後ほどEZRで読み込みたいデータの場所を指定する必要があるため,デスクトップなど自分が分かりやすい場所に保存しておくことをおすすめします!
準備2.EZRを起動 ⇒ CSVファイルの読み込み
CSV・ExcelファイルのEZRにおける読みこみ方は,以下で詳しく説明していますので,参考にしてみてください.今回はデータセット名はデフォルトのまま Dataset と名前をつけて読みこんでいます.
傾向スコアを用いた逆数重み推定の手順
傾向スコアを用いた逆数重み推定を行う手順は大きく3つに別れます.
- 傾向スコア&各群に所属する確率の逆数(重み)を計算する
- 重み付け前後で背景情報のバランスを確認する
- 重み付けを考慮しながらグループ間の比較を行う
1.傾向スコア&各群に所属する確率の逆数(重み)を計算する
まずは傾向スコアを推定してみましょう.このステップは基本的に傾向スコアマッチングの記事で紹介した内容と同じものになりますが,傾向スコアを計算すると同時に,各群に所属する確率の逆数(重み)を計算します.
また傾向スコアマッチングの記事で紹介したように,今回も傾向スコアはロジスティック回帰モデルを使って推定してみましょう.
今回は処置変数である treat_bin (1:処置あり, 0:処置なし) に関する傾向スコア(treat_bin=1となる予測確率)を背景情報である cnf1 と cnf2 から計算してみます.
- 名義変数の解析
- 二値変数に対する多変量解析(ロジスティック回帰)
- 目的変数 欄にカーソルをあてて処置変数 treat_bin をダブルクリック(※1)
- 説明変数 欄にカーソルをあてて交絡因子 cnf1 と cnf2 をそれぞれダブルクリック(※2)
- □傾向スコア変数を自動作成する にチェックを入れる
- □逆数重みづけ(IPW)のデータセットを作成する にチェックを入れる
- OK
※1.画面を開いた時点ですでに「目的変数」欄にカーソルが当たっているはずです
※2.treat_bin をダブルクリックしたら自動的に「説明変数」欄にカーソルが移動します
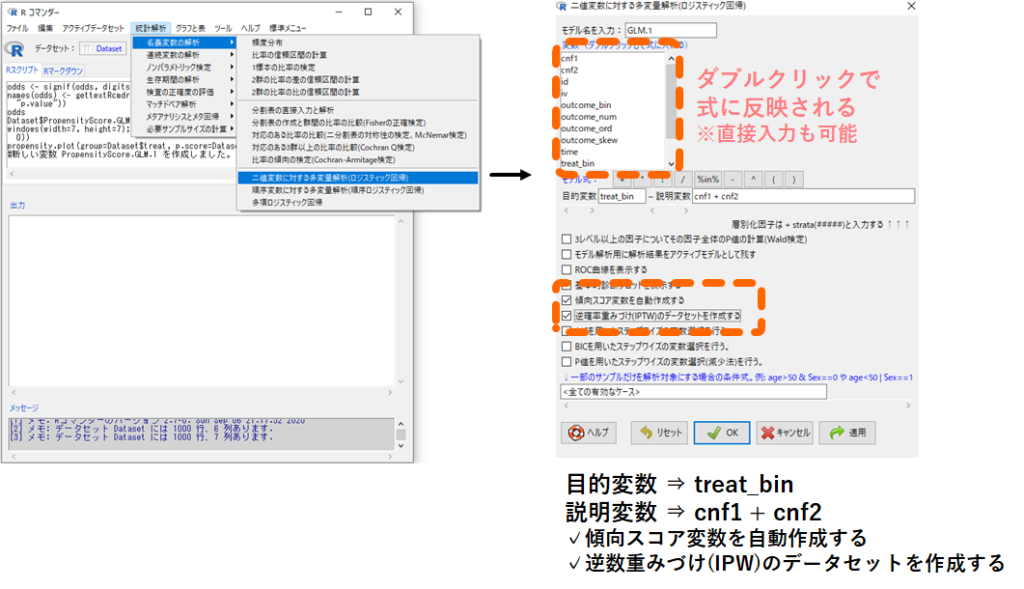
これで各対象者について,背景情報 cnf1 と cnf2 から計算された傾向スコアと逆数重みがデータDatasetに保存されているはずです.早速データの中身を以下手順で見てみましょう.
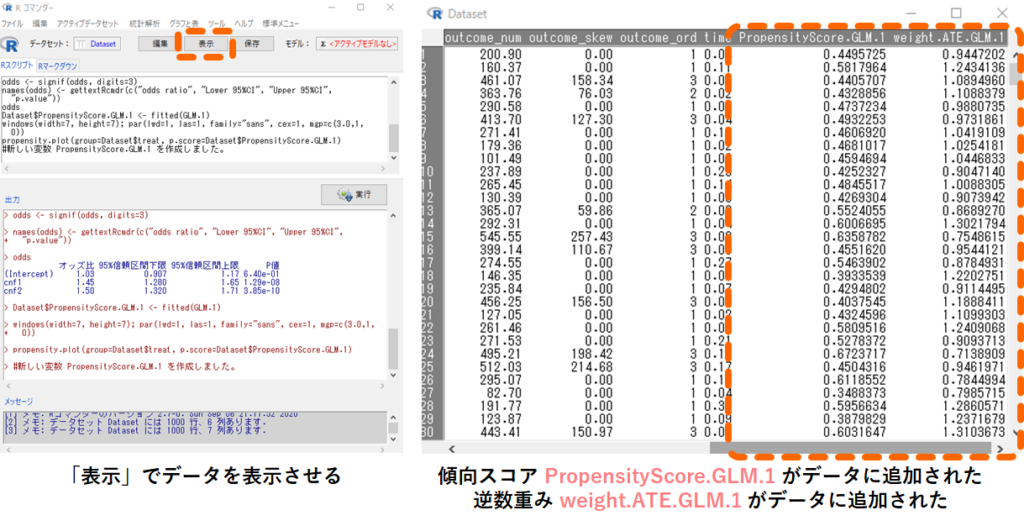
データの右端に「PropensityScore.GLM.1」という新しい変数ができていますね.これがcnf1とcnf2から予測した各研究対象者において処置が行われる確率であり,傾向スコアになります.
また「weight.ATE.GLM.1」という新しい変数も同時に作成されています.これは各グループに所属する確率の逆数となりますので,今回逆数重み法で利用する重みになります.
2.重み付け前後で背景情報のバランスを確認する
それでは重みづけ前後で,背景情報が揃ったかどうかを確認してみましょう.背景の揃い方の確認する方法も色々とありますが,今回は背景表の計算時に Standardized Mean Difference (SMD) を使ってみます.SMDは0に近いほどグループ間の背景情報の差が小さいと考えることができます.
傾向スコアマッチングの場合は,マッチング前のデータセットと,マッチング後のデータセットでそれぞれ背景表を作成し,同時にSMDを計算するだけでOKでした.しかし重みづけした背景表はEZRでは簡単に計算できないので,以下のようなステップを実行する必要があります.
- Datasetを使って重みづけしない背景表を作成する
- Rスクリプトを追記して重みづけデータを作成(背景表でのみ利用します)
- ###サンプルの背景データのサマリー表の出力### 以降を選択ハイライトして「実行」
Datasetを使って重みづけしない背景表を作成する
- グラフと表
- サンプルの背景データのサマリー表の出力
- [群別する変数] treat_bin, [カテゴリー変数] cnf2, [連続変数(正規分布)] cnf1
- [カテゴリー変数の検定方法] 独立性のカイ二乗検定, [標準化差を表示する] Yes
- OK
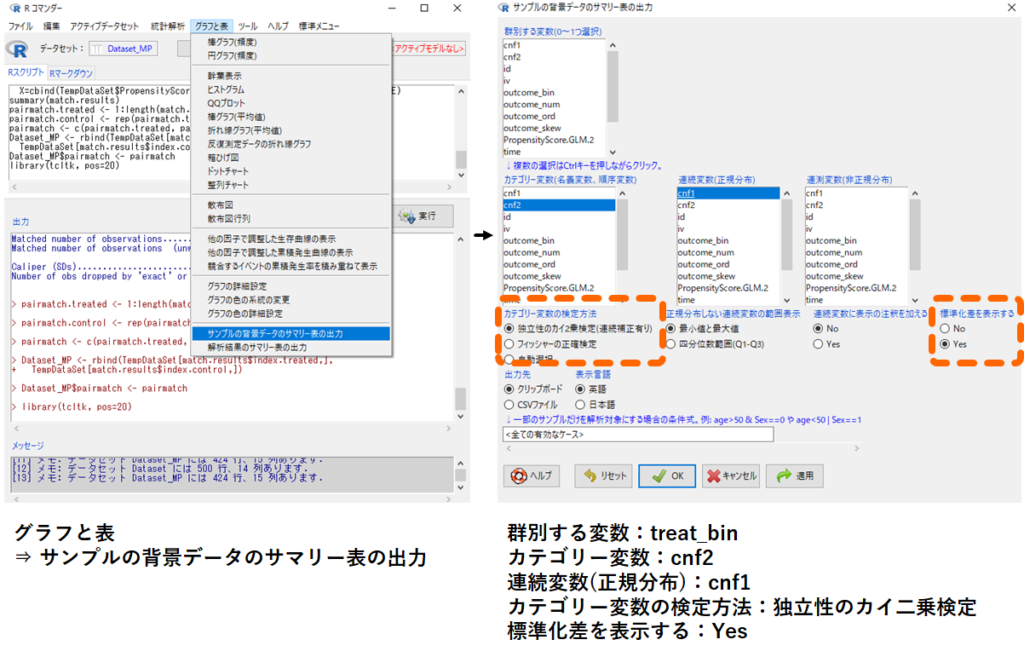
ここで得られる背景表は重みづけ前のものなので,当然両グループでバランスがとれていません.得られた表は後ほど,重みづけしたものと並べて眺めてみることにしましょう.
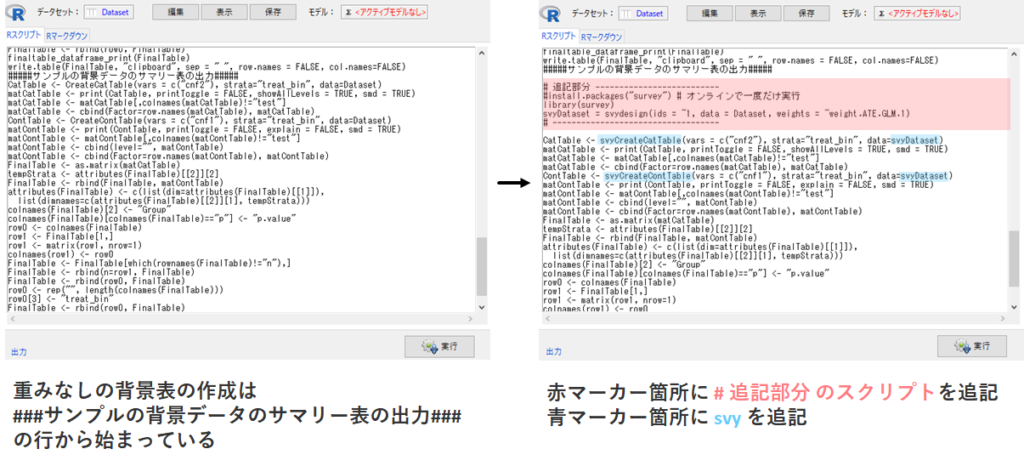
Rスクリプトを追記して重みづけデータを作成(背景表でのみ利用します)
ここでは重みづけをした背景表およびSMDを計算してみます.EZRには重みづけした背景表を自動で作成することができません.そこで,上記で作成した重みなしの背景表のRスクリプトに少し手を加えて,重みづけした背景表を作成してみたいと思います.
- ###サンプルの背景データのサマリー表の出力### の直下に以下のRコードをペースト
- 以下の4か所に修正を加える
- Dataset → svyDataset (※2か所!)
- CreateCatTable → svyCreateCatTable
- CreateContTable → svyCreateContTable
# 追記部分 --------------------------
install.packages("survey") # オンラインで一度だけ実行
library(survey)
svyDataset = svydesign(ids = ~1, data = Dataset, weights = ~weight.ATE.GLM.1)
# -----------------------------------
###サンプルの背景データのサマリー表の出力### 以降を選択ハイライトして「実行」
それでは上記の追記をしたコードを実行するために「###サンプルの背景データのサマリー表の出力###」意向をマウスで選択(青くハイライトされます)して,実行ボタンをクリックしてみましょう.
※ install.package(“survey”) 行の実行はオンライン環境が必要です.ここではパッケージのインストールをしています.インストール元を問われたら(国名などを選ぶ画面がでてきたら),0-Cloudを選んで進めてもらえば問題ありません.
作成した背景表を重みづけ前後で並べてみましょう.重みづけ前はSMDが0.2付近ですが,重みづけ後は非常に小さくなっていますね.実際にそれぞれの背景情報の値をみてみても,重みづけ後は各要素の割合や平均値のバランスが良くなったように見えます.これでグループ間での背景情報の不均衡を取り除くことができました!

3.重み付けを考慮しながらグループ間の比較を行う
重みづけによって背景も揃えることができたので,やっとこれでグループ間の結果変数をフェアに比べることができそうですね.次のステップでは,グループ間で結果変数を比べてみます.この時に注意しなければいけないことが,
- 処置効果の推定は重みづけを考慮して行う
- 一般化推定方程式などで標準誤差を推定する
という2点です.(1)については当然ですね.(2)については少し難しくなってくるので読み飛ばしてもらっても大丈夫ですが,IPW推定を行う際に単純な線形回帰モデルなどを利用してしまうと,重みさえ考慮していれば処置効果自体は問題なく推定できるのですが,推定値のばらつき具合を示す標準誤差という指標が過小評価されてしまいます.その点を考慮しつつ解析を行うことができる推定手法として,一般化推定方程式(Generalized Estimating Equation: GEE)があります.
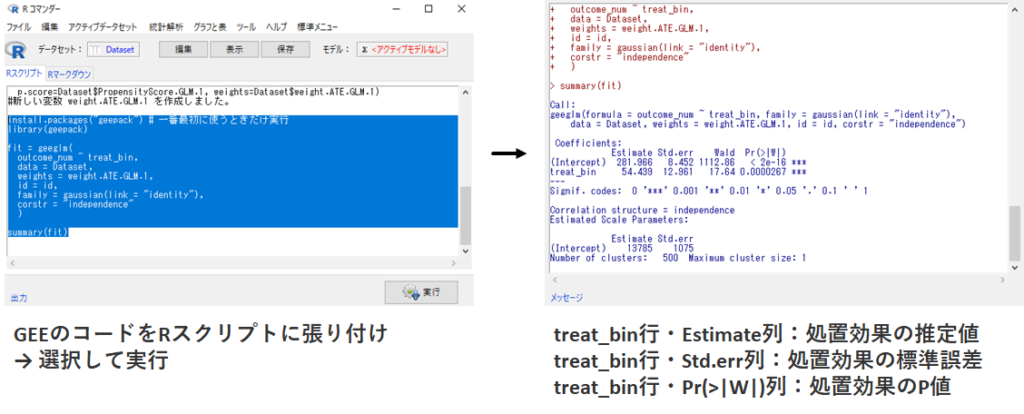
GEEを利用した解析はEZRではできませんので,以下のコードをRスクリプト画面に張り付けて実行する必要があります.以下では,結果変数である outcome_num を処置変数である treat_bin 間で比較する際に,処置確率の逆数である weight.ATE.GLM.1 で重みづけしています.
install.packages("geepack") # 一番最初に使うときだけ実行
library(geepack)
fit = geeglm(
outcome_num ~ treat_bin,
data = Dataset,
weights = weight.ATE.GLM.1,
id = id,
family = gaussian(link = "identity"),
corstr = "independence"
)
# 結果の出力
summary(fit)上記について簡単にポイントを説明しておきます.
- outcome_num ~ treat_bin: 結果変数 ~ 処置変数
- data = Dataset: 利用しているデータセット名を設定
- weights = weigth.ATE.GLM.1: 重み
- id = id: 各対象者を示す連番などの変数(各症例にユニークなものをあてること)
- family = gaussian(link = “identity”): 分布族.解析によって変える.
- corstr = “independence”: 相関行列.近接法で推定していて頑健なので気にしなくて良い.
family(分布族)については解析に利用する結果変数によって変える必要があります.生存時間分戦機を行う場合などは特殊なので,ここでは連続の場合と,2値の場合だけを出しておきます.
| 結果変数の尺度 | GEEにおける分布族(リンク関数) |
| 連続(線形回帰モデルを利用したいような場合) | gaussian(link = “identity”) |
| 二値(ロジスティック回帰モデルを利用したいような場合) | binomial(link = “logit”) |
解析やデータに応じて,それぞれの変数の名前を書き換える必要があります.もし違うデータや変数を利用する場合には,データ内の変数名とコード内の変数名が完全に一致しているかどうか,しっかりと確認するようにしてみてください.
結果としては,重みづけをした後の処置効果の推定値は 54.439 となり,処置によって結果変数であるoutcome_numは54.498だけ上昇することが分かりました.この結果については,既にcnf1やcnf2による交絡の影響は受けていないと考えることができます.
これでIPWの解析は終了です.EZRの機能だけではカバーしきれないところがあるので,すこし作業が煩雑になりましたが,慣れれば難しいものではありませんので,ぜひご自身のデータでもチャレンジしてみてください.
最後にひとつだけコメントを添えておくと,今回IPWで推定した処置効果は,厳密には「全ての対象者における平均的な処置効果(Average Treatment Effect: ATE)」と呼ばれるものです.本来データには各対象者は処置を受けた・受けていないのどちらか一方のグループに所属していますが,仮想的に「対象者全員が処置をうけた場合・全員が処置をうけなかった場合」を考えた時にどれくらいの効果があったのかを考えているということです.同じ対象者同士でくらべているので,背景も当然そろいますよね.これがIPWを含む因果推論手法における反実仮想というコンセプトになります.
これに対して「実際に処置をうけた対象者における平均的な処置効果(Average Treatment effect on the Treated; ATT)」という考え方もあります.関心があるのは実際に処置をうけた人たちであり,その人たちがもし処置を受けていなかった場合と比べると,どのくらい効果があったのだろうか?ということを考えるということですね.このあたりはまた面白いところなので,また別の記事で紹介します.
今回の内容を通して,以下の論文が非常によくまとまっていて分かり易いので,良ければ参考にしてみてください.
Austin PC, Stuart EA. Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Stat Med. 2015 Dec 10;34(28):3661-79. doi: 10.1002/sim.6607. Epub 2015 Aug 3. PMID: 26238958; PMCID: PMC4626409.
まとめ
今回はEZRを用いた傾向による逆数重み推定法(IPW)の解析手法に関する一連の流れについて紹介しました.EZRを使えば難しい操作なく傾向スコアの推定と重みの計算が可能です.
重みづけを行った後の処置グループ間の背景を比べたり,重みづけをしながらグループ間で結果変数を比較する際には,Rのコードを書き足す必要がありましたが,この記事の解説通り進めてもらえば問題ありません!
またEZRで使える因果推論系の機能も日々アップデートされているので,今後も楽しみですね.
EZR開発者の先生が出されている書籍や,因果推論についてもっと専門的なところまで勉強したいという方にお勧めの書籍も以下に紹介しておきます.
- (因果推論をRで学びたい方向け)統計的因果推論の理論と実装 (Wonderful R)
- (因果推論をPythonで学びたい方向け)つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門
- (因果推論の理論も学びたい方向け)調査観察データの統計科学: 因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)





コメント
【EZR】傾向スコアによる逆数重み推定(IPW)の解析手順【図解】を拝見させていただきました。
“Rスクリプトを追記して重みづけデータを作成”の項目を表示されている通りに行ってみたのですが、重みづけ前とまったく同じ結果が返って来て、重みづけが反映されていない結果となってしまいます。メッセージ項目に“エラー:オブジェクト ‘svyDataset’ がありません”と表示されております。何度か確認しながらやり直し、サイトに表示頂いているプログラム部分も照らし併せましたが、原因がわかりません(svyも入力しております)。
何かうまく重みづけされない問題があるのでしょうか?ご教授いただければと幸いです。
是非ともよろしくお願いいたします。
ご質問いただきありがとうございます.
こちらでも再度内容を確認いたしますが,以下ご参考まで,ご確認頂けましたら幸いです.
このコードを実行するためには,以下のコードを事前に実行する必要があります.
特に1行目はインターネット環境で実行する必要があるのですが,問題なく実行が完了できていそうでしょうか?
もし赤文字でエラーが生じているようであれば,エラーの内容をみて対処が必要になると思います.
install.packages(“survey”) # オンラインで一度だけ実行
library(survey)
記事を拝見させていただきました。
現在行っている研究に必要で、穴があくほど読み込ませていただいております。
IPTWの解析終了後、重みづけを行ったデータ群間でt検体を行ないたいのですが、お時間のある際にその方法についてご教示いただけないでしょうか?
ありがとうございます.
これはまた近日中に追記しますね.遅くなってしまいすみません.
御執筆ありがとうございます。サイト内のcsvファイルがダウンロードできないようになっております。ご確認いただけませんでしょうか。
ご報告ありがとうございます.
少し忙しくしていまして,修正が遅くなりました.
ダウンロード可能となるように修正しましたので,ご確認お願いいたします.
【EZR】傾向スコアによる逆数重み推定(IPW)の解析手順【図解】
わかりやすい説明で参考にさせていただいたのですが、私も上記の質問者様と同様に
“エラー:オブジェクト ‘svyDataset’ がありません” と表示され、重み付け前の背景表が表示されます。1回目はインストール画面が表示され、0-cloudを選択しました。自分のデータセットがおかしいのかと考え、robustwife_allのCSVファイルをダウンロードさせていただこうと思ったのですが、権限がありませんと表示され、ダウンロードできません。ご確認よろしくお願いします。
データセットについて,アップロードしなおしました!
もしかすると,ロジスティック回帰モデルを何度か実行していませんか?EZRでは回帰モデルを実行するたびに,結果が保存されるオブジェクト名の末尾の番号が増えていきます.
それと同時に,データに追加されるPropensityScore変数や,Weight変数の末尾の番号も変わってしまいます.
今回は末尾の番号が1の場合のスクリプトを利用しています.以下のweight.ATE.GLM.1の末尾の番号を,ご自身のデータに保存されたweightの番号に替えて実行して頂くとどうでしょうか?
# 追記部分 ————————–
install.packages(“survey”) # オンラインで一度だけ実行
library(survey)
svyDataset = svydesign(ids = ~1, data = Dataset, weights = ~weight.ATE.GLM.1)
# ———————————–