【統計コンセプト】傾向スコアを数式なしで理解する【図解】

記事の要約：傾向スコアを数式なしで理解する【図解】

この記事で学べること

• 傾向スコアとはなにか？
• 傾向スコアを使った解析手法の種類
• EZRによる傾向スコアの推定方法

この記事の結論

• 傾向スコアとは治療などの処置変数をその他の情報から予測したもの
• 最終的な目的は傾向スコアの推定ではなく，傾向スコアを使って処置の効果を推定すること
• 傾向スコアはEZRで簡単に計算可能
• 以下の書籍がおすすめ

傾向スコアとは？

おそらくこの記事を見ている皆さんは，「傾向スコア」という言葉は聞いたことがあっても，実際にその内容についてはよくわからない…あるいは実装方法に悩まれている方が多いのではないかと思います．

この記事では，傾向スコアとはなんなのか，何のために利用するのか，どのように利用できるのか，また実際にデータを使った計算手順まで説明していきたいと思います．

傾向スコアとは？

そもそも，傾向スコアってなに？っていうところからお話したいと思います．

傾向スコアというのは，ざっくり言うと，治療や政策など（これを”処置”と呼びます）の効果を推定する際に，比較するグループ間の背景情報の不均衡よるバイアスを取り除く手法のひとつです．

「比較するグループ間の背景情報の不均衡よるバイアス」を専門用語で交絡と呼びますが，これがまず何なのか説明していきたいと思います．

交絡とは？

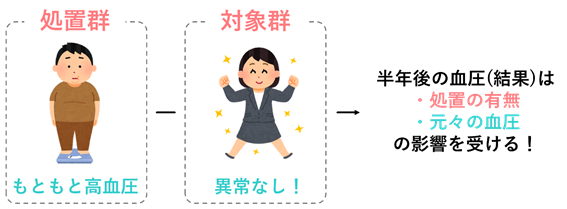
交絡とは，比較を行うグループ間で処置以外の因子や条件が異なっているときに生じるバイアスのことを指します（バイアスというのは，神のみぞ知る真の処置の効果から，ご自身がデータから推定した効果がどの程度ずれているかという指標です）．

例えば治療をうけたグループ（処置群）と治療をうけなかったグループ（対照群）で半年後の血圧を比較する例を考えてみます．このときに，治療を受けたグループでは，治療を受けなかったグループに比べて，もともと血圧が高い患者さんが多かったとします．つまり，治療を行う段階ですでに比較するグループ間で，処置以外の因子が偏ってしまっている状況です．

この状態で単純に半年後の血圧をグループ間で比較するとどうなるでしょうか？もし半年後の血圧は両群間で同じであった場合，比較するグループ間でアウトカムである半年後の血圧が変わらないので治療の効果（処置効果）は0である，と考えられるでしょうか．

ここまでのストーリーを知っている皆さんは「今回は薬によってある程度血圧が下がったけれど，治療を受けた患者さんはもともと血圧が高かったために，半年後の血圧がグループ間で同じになったのだろう」と推察できますよね．つまり，処置以外の因子（もともとの血圧）が比較グループ間で異なっていたために，処置の効果は本当はあったにも関わらず効果がない（半年後の血圧が比較グループ間で変わらない）と推定してしまっているのですよね．この現象が交絡であり，交絡を生じさせる因子のことを交絡因子と呼びます．交絡はバイアスを生じさせる要因であるため，処置の効果を正しく推定するためには，最大限とりのぞく努力をしなければなりません．

交絡をどうやってとりのぞく？

この交絡はどうやって取り除くのでしょうか？交絡を取り除く方法は大きく以下の２つに分けられます．

1. 研究デザインによる対処 ⇒ 無作為化比較試験（RCT: randomized controlled trial）等
2. 解析手法による対処 ⇒ 多変量回帰モデル，因果推論手法等

まず（１）は「そもそも交絡が起こらない状況設定で研究をしよう」というものです．上記で説明した通り，交絡は関心のある処置（治療など）以外の因子が比較グループ間でずれるために起こる現象でした．例えば先ほどの血圧の例だと，医師はもともと血圧の高い患者さんに治療を行っていたために，治療をうけたグループに血圧の高い患者さんが多いという偏りが生じていました．逆に言うと，もともとの血圧や患者さんの状態などを全く気にせずに治療をするかどうかを完全にランダムに決めてしまっていれば（普通の臨床では認められることではありませんが…），そのような偏りはでないと考えられますよね．

そこで一般の臨床などでは認められませんが，研究を目的として，処置の割り当てをランダムに決めてしまおうというのがRCTです．処置の割り当てを完全にランダムに決めてしまうため，処置を受けたグループと受けていないグループにおける処置以外の因子が平均的に揃えることができます．処置以外の因子が平均的に揃っている状況であれば，アウトカムのグループ間の差（半年後の血圧のグループ間の差）は，処置だけに依存したものである，つまり交絡の影響をうけない処置そのものの効果であると理論的に考えることができます．

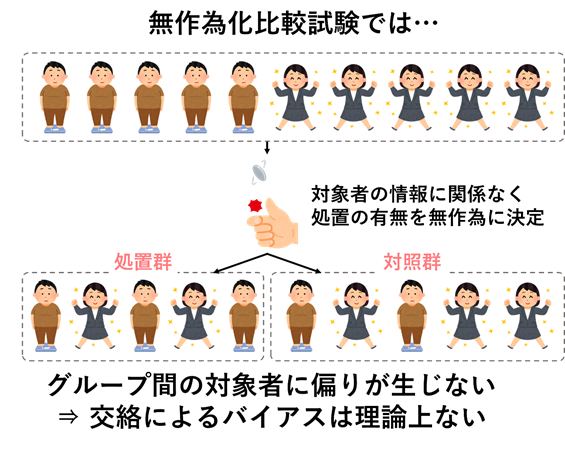
このように交絡の問題をとりはらってしまえる研究デザインがRCTであり，交絡を取り除くという点においては，非常に有用な対策になります．

しかしRCTでは治療をランダムに行うために倫理的な問題が出てきたり，ものによってはそもそも実現可能性の低い場合もあります．ここでは詳しく説明しませんが，交絡以外にも研究において問題になる要因はたくさんありますし，それらが解決できない場合にはRCTを行うことが不適当であることもあります．

そこでRCTのような実験的なデザインで得られた情報ではない，電子カルテや公開データのような既存の情報を用いた研究について考えることにします．しかしこれらのデータにおいては，上述したような交絡の問題が付きまといます．

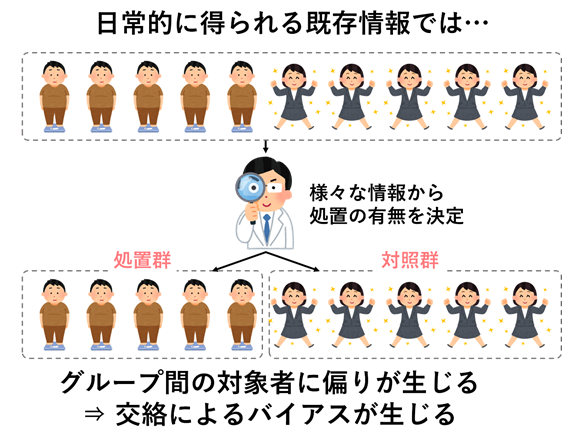
それを解析においてどうにか解決しようというのが（２）解析手法による対処になります．先ほどの例だと比較グループ間で半年後の血圧が変わらなかったとしても，皆さんの頭の中では「それは治療に効果がなかったということではなく，薬によってある程度血圧が下がったけれど，治療を受けた患者さんはもともと血圧が高かったために，半年後の血圧がグループ間で同じになったのだろう」という計算ができていましたよね．つまりもともとの血圧の高さというものを考慮した計算をしていたということです．これを統計解析にも反映させてあげれば，交絡の影響を取り除いた治療効果が推定できそうですよね．

その際に利用されることの多い解析手法として，多変量回帰分析や，操作変数法などの因果推論と呼ばれる領域に属する解析手法があります．これらの基本的な目的としては「処置以外の因子の影響をとりのぞいた上で処置効果を推定する」ということです．この時に「処置以外の因子」をどれだけ・どのように考慮するのかがとても大事になります．

傾向スコアをつかって交絡を取り除く

交絡を取り除く方法

上記の通り，そもそも交絡がなぜ起こるのか？の答えは「比較するグループ間で処置以外の条件が異なるため」ということになります．では交絡を取り除くために何をすればよいか？と聞かれたら「比較するグループ間で処置以外の条件を等しくする」という回答が思い浮かびますよね．まさにそれが正解です．

では比較するグループ間の条件を等しくするにはどうすれば良いでしょうか？最も単純に考えるのであれば，処置群と対照群に類似した条件の研究対象者に入ってもらえばよいですよね．たとえば，処置をうけている50歳，60kg，150cmの女性が研究に参加した場合には，処置をうけていない50歳，60kg，150cmの女性をあてがえばよいのです．これを繰り返していけば必然的に，処置グループにも対照グループにも同じような研究対象者が含まれることになりますよね．これで比較するグループ間で条件が整いましたので，交絡は起こり得ません．やりましたね！

…でもここで少し違和感を感じませんか？

処置をうけている方と処置をうけていない方で，全く条件が同じような方を探し当てるのって結構大変だと思いませんか？上記のように年齢，体重，身長，性別くらいであれば可能かもしれませんが他にも収入，病気の既往歴，家族構成などなど，ひとが処置をうけるかどうかの決定には非常に多様な要素が絡み合ってくるはずです．それらを全て等しくすることは実際には不可能ですよね．

そこで提案されたのが「傾向スコア」です．傾向スコアとはその名の通り「処置をうける傾向を反映したスコア」になります．処置をうけるかどうかという傾向は，上述したように，非常に多様な要素から成り立っています．それらをひとつひとつ条件づけていては，とてもじゃありませんが実現可能性が低くなってしまいます．

ではそれらの処置を決定づける多様な因子をひとつのスコア（スコア）に落とし込んでしまえば分かり良いではないか？と考えられるわけです．種々の情報を考慮したひとつのスコアだけであれば，処置グループと対照グループから同じスコアをもった対象者を選んでくることはそんなに難しそうではありませんよね！複数の情報がひとつの点数にまとまる，これがまさに傾向スコアを使う非常に重要なポイントになります．

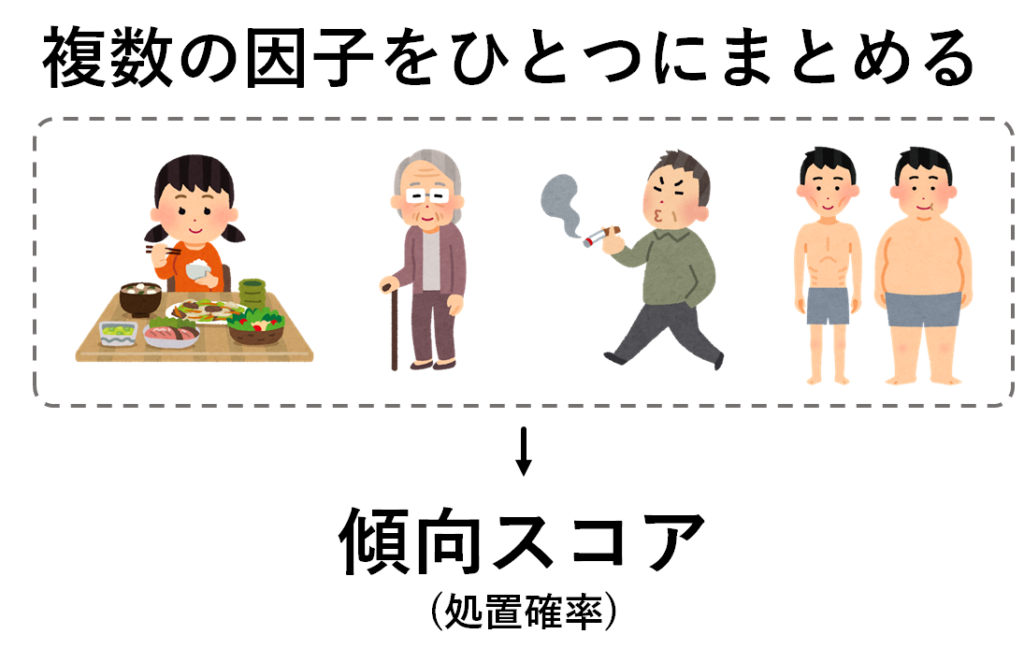
傾向スコアの計算手順

それでは傾向スコアはどうやって計算するのでしょうか？上記では傾向スコアは「処置をうける傾向を反映したスコア」であると説明しましたが，もう少し具体的にいうと「処置以外の情報から予測した処置をうける確率」になります．

例えば上記の高血圧治療の例においては，治療を受けるかどうかは，事前に高血圧の既往歴があるかどうかによって変わってくることが考えられ，もちろん高血圧の既往歴をもつ患者さんの方が，治療を受ける確率，つまり傾向スコアは高くなります．これを高血圧の既往歴のみでなく，測定されている他の因子についても同時に考慮していきます．それらを鑑みた合計的な点数として傾向スコアが計算されるというわけです．

この処置をうける確率をどうやって計算するかというと，色々な方法がありますが，最も一般的な方法がロジスティック回帰モデルを用いた方法です（他の回帰モデルを用いた方法や，機械学習を利用した方法などもありますが，それはまたおいおい…）．ロジスティック回帰モデルについてはここではざっくりと「イベントの有無や処置の有無などの二値変数を応答変数とした解析モデルであり，イベントや処置が有となる確率を予測できるもの」と理解しておいてもらって問題ありません．

この傾向スコアはEZRを使って簡単に計算ができますので，以下に参考データを用いた手順を示しておきます．

今回は実際のデータを使うのではなく，傾向スコア計算の計算のために実験的に作成した以下のデータを利用しています．このデータは以下の手順１でダウンロード可能です．

id	cnf1	cnf2	treat	outcome
1	0.077303	0.850043	0	67.46798
2	-0.29687	-0.92531	0	47.10014
3	-1.18324	0.893581	1	76.63003
4	0.011293	-0.94101	1	71.73025
5	0.991601	0.538952	0	74.70814
6	1.593967	-0.18197	1	95.27978
7	-1.37271	0.891768	1	73.85734
8	-0.24961	1.329208	1	89.87022
9	1.159425	-0.10347	1	89.48509
10	-1.11422	0.615065	0	53.55731

• 対象症例1000名
• 交絡因子１（cnf1）：測定されている交絡因子
• 交絡因子２（cnf2）：測定されている交絡因子
• 結果変数（outcome）：100点までの点数等の連続型変数
• 真の処置変数の結果変数における効果：+20点

それでは早速傾向スコアを計算してみましょう．

手順１．以下のデータセットをダウンロード

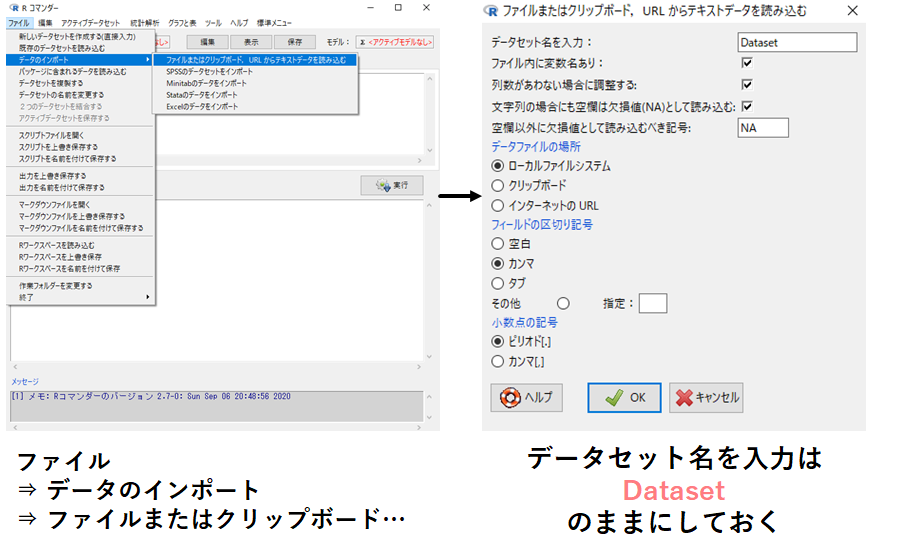
手順２．EZRを立ち上げて以下手順でデータを読み込む
ファイル
⇒ データのインポート
⇒ ファイルまたはクリップボード，URLからデータを読み込む
⇒ データセット名をデフォルトのまま「Dataset」でOK

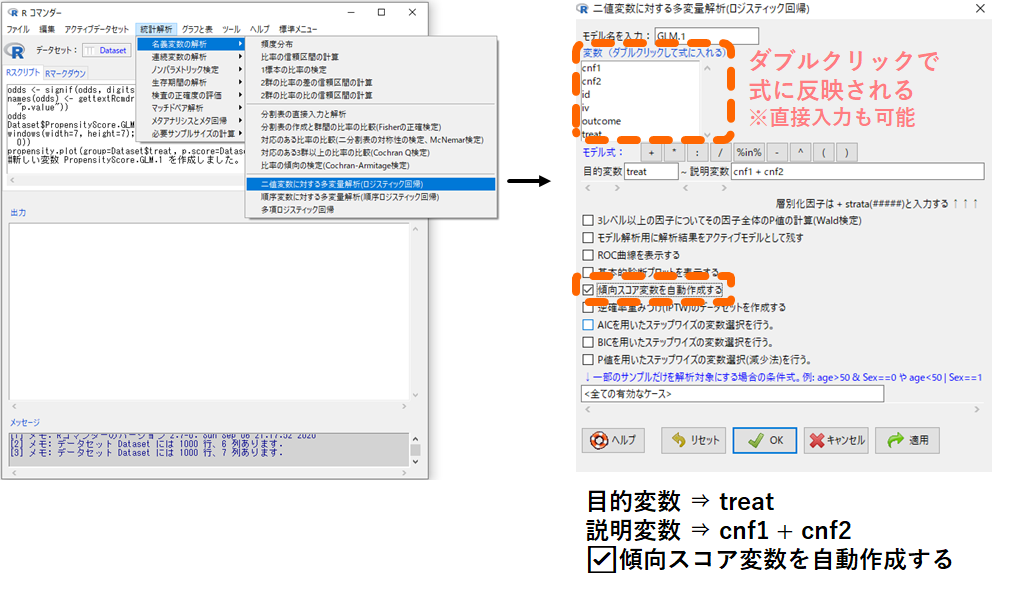
手順３．以下手順でロジスティック回帰モデルを用いて傾向スコアを推定
統計解析
⇒ 名義変数の解析
⇒ 二値変数に対する多変量解析（ロジスティック回帰）
⇒ 「目的変数」欄にカーソルをあてて処置変数「treat」をダブルクリック（※1）
⇒ 「説明変数」欄にカーソルをあてて交絡因子「cnf1」「cnf2」をそれぞれダブルクリック（※2）
※1．画面を開いた時点ですでに「目的変数」欄にカーソルが当たっているはずです
※2．Treatをダブルクリックしたら自動的に「説明変数」欄にカーソルが移動します
⇒ 「□傾向スコア変数を自動作成する」にチェックを入れる
⇒ 「OK」をクリック

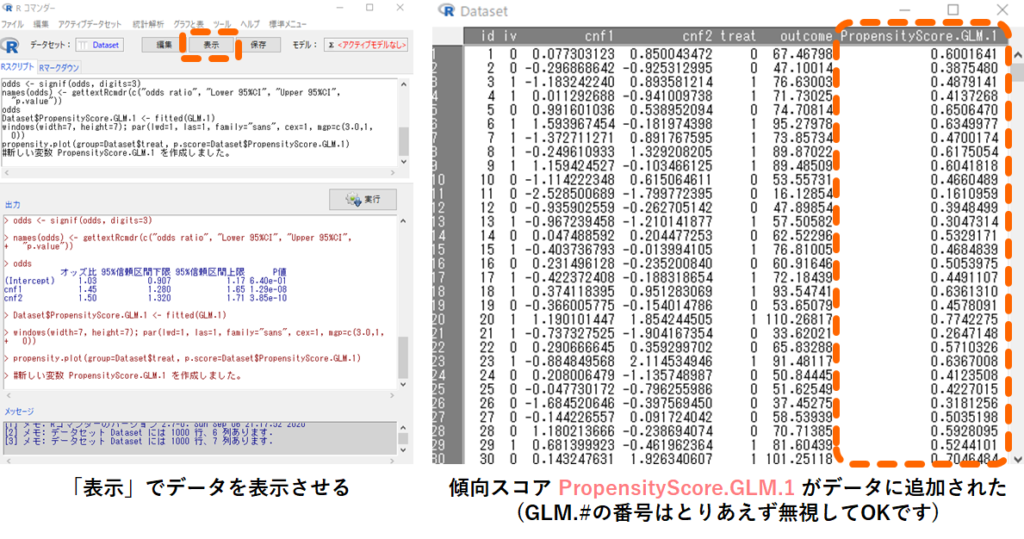
これで各研究対象者について，交絡因子cnf1とcnf2から計算された傾向スコアがデータDatasetに保存されているはずです．早速データの中身を以下手順で見てみましょう．データの一番右端に「PropensityScore.GLM.1」という新しい変数ができていますね．これがcnf1とcnf2から予測した各研究対象者において処置が行われる確率であり，傾向スコアになります．（※GLM.#の番号は何回目に推定を行ったものかを示しているだけなので，気にしなくても大丈夫です．）

傾向スコアを利用してバイアスを除去する解析手法

さて，これで傾向スコアを実際に計算することができました！しかし，傾向スコアを利用した解析は，傾向スコアを計算するところがゴールではありません．この傾向スコアを利用して処置グループと対照グループの処置以外の背景情報を揃えつつ，処置の効果を推定しなければいけません．

傾向スコアを用いた処置効果の推定方法は種々提案されています．

代表的なものとしては，上記に挙げていたように処置グループと対照グループで類似した傾向スコアを持った研究対象者同士をマッチングすることによって，比較グループ間の背景因子を揃える「傾向スコアマッチング推定法」があります．マッチングした後のデータでは，比較グループ間で背景がそろっていることが確認できるため，非常に分かりやすく多くの方に親しまれている方法です．（EZRにおける傾向スコアマッチングの解析手順はこちらの記事で紹介しています．）

また他にもよく利用される手法として，処置確率逆数重み推定法（inverse probability of the treatment weighting estimation：IPW）があります．これは処置をうけた対象者は処置をうける確率の逆数で人数をかさ増しして，処置をうけなかった対象者は処置をうけない確率の逆数で人数をかさ増しする方法です．このようにそれぞれのグループに属する確率の逆数で人数をかさ増しする（重みづけする）と，不思議なことに両グループに同じような背景因子をもった対象者が同程度存在するような状況を想定することができます．

またその他にも，層別化推定法や，二重頑健推定法などなど…本当に色々な手法が提案されています．実はそれぞれの手法によって推定している効果はちょっとずつ異なったり，目的がそもそも違っていたりします．

ここで簡単に説明しているだけではイメージしづらいと思いますので，別の記事にてそれぞれの推定手法のコンセプト，実際にみている効果についてなどの詳細，またその解析手順について詳しく説明していこうと思います．

傾向スコアの推定時に気を付けること

処置以外の因子をひとつの変数に置き換える傾向スコア，色々な使い方ができそうですよね．そんな便利な傾向スコアですが，推定のときに意識した方が良いことが数点ありますので，簡単に紹介しておきます．

1. 傾向スコア推定に含める変数は処置が実施されるよりも前の情報のみとする
2. 傾向スコア推定では結果変数に関与する因子を優先的に考慮する
3. 傾向スコア推定には処置のみに影響している因子（操作変数）は含めない

（１）については，非常に単純な理屈なのですが，例えば上の例の高血圧に対する治療の例であれば，結果変数は半年後の血圧となります．つまり「治療⇒半年後の血圧」という関係について治療の効果量を考えているわけです．もしこの研究において「治療3か月後の血圧」も測定していたとします．もし傾向スコアの推定にこの「治療3か月後の血圧」を含めるとどうなるでしょうか？答えは治療効果を過小評価してしまう方向にバイアスが生じることが考えられます．

「治療⇒半年後の血圧」という関係を細やかにみると実は「治療⇒3か月後の血圧⇒半年後の血圧」という流れになっているはずです．つまり治療は3か月後の血圧に影響を与え，その結果さらに半年後の血圧に影響を与えている，ということになります． 3か月後の血圧は，処置変数である治療と結果変数である半年後の血圧の間に介在する「仲介因子」であることが考えられます．もしこの仲介因子について，処置グループと対照グループで揃えてしまったらどうなるでしょうか？せっかく治療によって得られた3か月後の血圧という効果をなかったことにしてしまいますよね．3カ月間で得られた効果が差し引かれてしまうため，結果的に6か月間で得られた効果量をも過小評価してしまうことにつながるのです．これを防ぐためにも，処置が行われたあとに起こった現象，つまり処置によって引き起こされた現象については傾向スコアに含めないのが無難です．

（２）と（３）については，傾向スコアを推定する際には，結果変数と関連の強いものを優先的に考慮して，処置のみと関連するものは含めないということです．これは少し不思議に思われるかもしれません．傾向スコアというのは，各対象者の背景にある因子から処置をうける確率を予測したものと説明されていたにも関わらず，傾向スコアを推定する際には処置をよく説明するような因子ではなく，結果変数に関連するものを入れろと言っているのですから．

これは結構専門的なお話になるのですが…交絡によるバイアスというのは，比較グループ間で偏りを持った因子と結果変数が相関することで結果的に起こるものなので，極論を言うと結果変数に影響を与えないものは交絡を起こさないし，無視してOKです．

さらに言うと，処置と強く関連していても結果変数と関連しない因子（これを操作変数と呼びます）は傾向スコアの推定に含めるべきではないと，理論的に示されています．処置と強く関連する因子を傾向スコアで考慮すれば，傾向スコアの予測精度はもちろん高くなりますが，それは結果的に処置効果の推定にとって実は重要ではありません．逆に，操作変数のように結果変数に全く関係しないようなものを傾向スコアの推定時に考慮してしまうと，処置効果の推定の精度が悪くなってしまうという問題があります．また反対に，処置に全く関連しなくても，結果だけに関連しているような因子を考慮することによって，処置効果の推定の精度を向上させることができることも示されています．

この辺りは非常に専門的な内容になるのですが，一応そういったことがあるのだな，とまずは掴んでもらえれば問題ありません．もっともっと詳細に理論的な部分まで知りたい方は，以下の参考図書をぜひ読んでみてください！

因果推論おすすめの書籍

• 調査観察データの統計科学
• 統計的因果推論
• つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門
• 統計的因果推論の理論と実装