記事の要約:EZRによる操作変数法の解析手順【図解】
この記事で学べること
- 操作変数法とはなにか?
- 操作変数法の直感的な理解
- 操作変数法のEZRにおける解析手順
この記事の結論
- 操作変数法とは治療などの処置効果をバイアスなく推定する手法のひとつ
- 処置の割り当てを「操作変数で説明できる部分」と「それ以外で説明できる部分」に分けて考えることが肝
- 実際の解析はRで簡単に実行可能!(※実際には厳しい仮定が必要なので注意が必要ということも念頭に置いておいてください)
- 以下の書籍がおすすめ
- (因果推論をRで学びたい方向け)統計的因果推論の理論と実装 (Wonderful R)
- (因果推論をPythonで学びたい方向け)つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門
- (因果推論の理論も学びたい方向け)調査観察データの統計科学: 因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
操作変数法とは?
おそらくこの記事にたどり着いた方は「操作変数法」なる解析手法の名前を聞いたは良いものの,何のことかさっぱり分からず,本を読んでもいまいち理解できず,結局何ができるのかさえよくわからなかっ…という迷える方々が多いのではないかと思います.
…その気持ち,よく分かります.
ここではそんな方のために,操作変数とは何なのか?何ができるのか?を直感的につかんでもらえるように解説をしたいと思います.
また「実際に使って解析してみたい!」という方のために,実際のデータを用いた解析手順までを説明したいと思います!
操作変数法とは?
そもそも,操作変数法ってなに?っていうところからお話したいと思います.
操作変数法というのは,ざっくり言うと,治療や政策など(これを”処置”と呼びます)の効果を推定する際に,比較するグループ間の背景情報の不均衡よるバイアスを取り除く手法のひとつです. では,「比較するグループ間の背景情報の不均衡よるバイアス」を専門用語で交絡と呼びますが,これがまず何なのか説明していきたいと思います.
交絡とは?
交絡については,以下の記事で例を挙げて説明しています.簡単にまとめると「比較するグループ同士の元々の状態が違うとフェアに比較できないよね」という問題です.
もともと具合の悪い人ばかりが治療を受けていた場合,治療群と非治療群で死亡リスクを比べると,治療群に不利な結果がでてしまいますよね.そのようなどちらかのグループに不利な状態で比較をしても意味がないので,そのような背景情報の不均衡は,事前に取り除いてあげなければいけません.
以下の記事ではこの交絡という困った問題を,どうやって解決するのか,その基本的な考え方についても説明しています.
交絡をどうやってとりのぞく?
上記の記事で交絡を取り除く一般的な方法として,以下の2つを挙げました.
- 研究デザインによる対処 ⇒ 無作為化比較試験(RCT: randomized controlled trial)
- 解析手法による対処 ⇒ 多変量回帰モデル,因果推論手法等
2の解析手法による対処として利用されることの多い解析手法として,多変量回帰分析や,操作変数法などの因果推論と呼ばれる領域に属する解析手法があります.
これらの基本的な目的としては「処置以外の因子の影響をとりのぞいた上で処置効果を推定する」ということです.この時に「処置以外の因子」をどれだけ・どのように考慮するのかがとても大事になります.そしてここが操作変数法の肝となる部分になります.
未測定交絡と操作変数法
上記で説明した多変量回帰分析などで,例えばすでに取得されている処置以外の情報を10個考慮して解析を行いました.つまり処置の効果を純粋に推定するために,年齢や性別,社会的な情報など10個の因子について影響を取り除いたということです.これで処置効果をバイアスなく推定できたと言えるでしょうか?もしかしたら11個目の因子でバイアスが起こっているかもしれませんよね…ということでとってもとっても頑張って100個の因子を考慮してみました.これなら十分でしょうか?いやもしかすると101個目でバイアスがかかっているかもしれませんよね…
このように既存情報を用いた研究では,測定されていない,あるいは測定されていても解析で考慮されていない因子の影響は取り除くことができません.これを「未測定交絡」と呼んだりしますが,つまりは「無作為化比較試験をしていない限り,全ての因子の影響を取り除くことは理論的にはほぼ不可能」という指摘をうけるわけです.厳しいですよね.
それでは既存情報を用いた研究でバイアスなく平均処置効果を推定することは不可能なのでしょうか?ここでやっと操作変数法がでてきます.操作変数法の最大のメリットを先に述べると「未測定な交絡因子の影響も全てとりのぞいた処置効果の推定が可能である」という点が挙げられます.「え,集めてもいない交絡因子の影響もとりのぞけるの?ファンタジーの話?」と思われた方も多いと思います.よくわかります.頭の方々はすごいこと考えますよね. それでは操作変数法がどういう仕組みで成り立っているのか,感覚的に説明をしていきたいと思います.まずは操作変数法の説明をするために,それぞれの因子がどのような関係になるのかを図示しておきます.
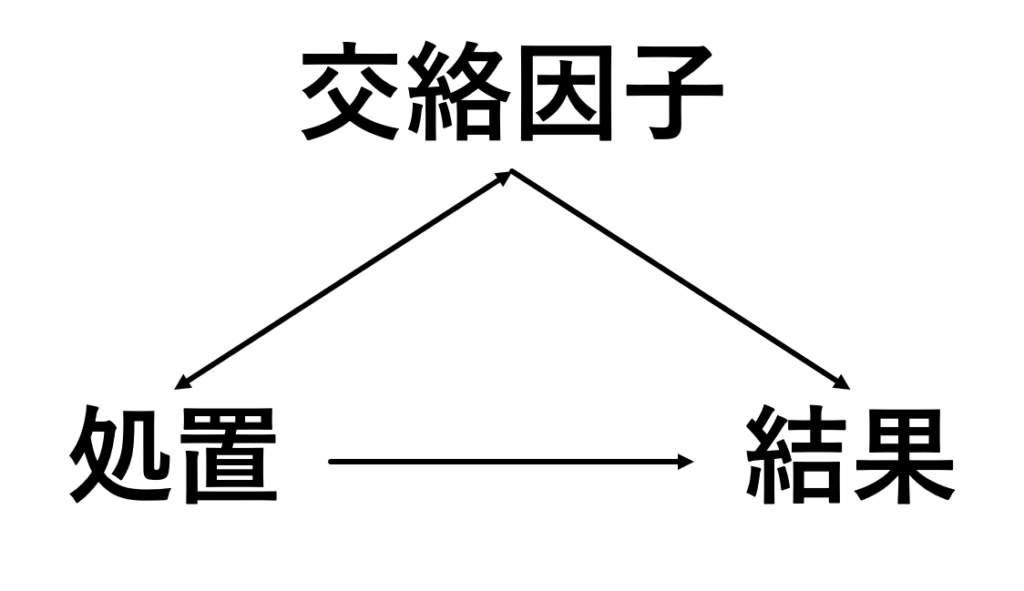
まず,興味の関心となる処置は,当然結果に影響するとしておきます(=処置は結果に影響を与えて).また交絡因子は処置を受けるかどうかの判断材料となり(=交絡因子と処置は関連している),さらに交絡因子は結果にも影響を与える(=交絡因子は結果に影響を与える)という構造を考えます.先ほどの例だと,治療グループが「処置」,半年後の血圧が「結果」,治療を行う前のもともとの血圧が「交絡因子」となり,治療をすれば半年後の血圧には影響する(処置⇒結果)が,治療を受けたグループにはもともと血圧が高い人が多く(処置⇔交絡因子),もともと血圧が高い人は半年後の血圧も高いままになりやすい(交絡⇒結果)ということになります.
ここでもう1つ因子を考えてみます.そう今回のメインである「操作変数」です.操作変数とは,
- 処置と関連する
- 結果と関連しない
という変数になり,図では以下に位置します.
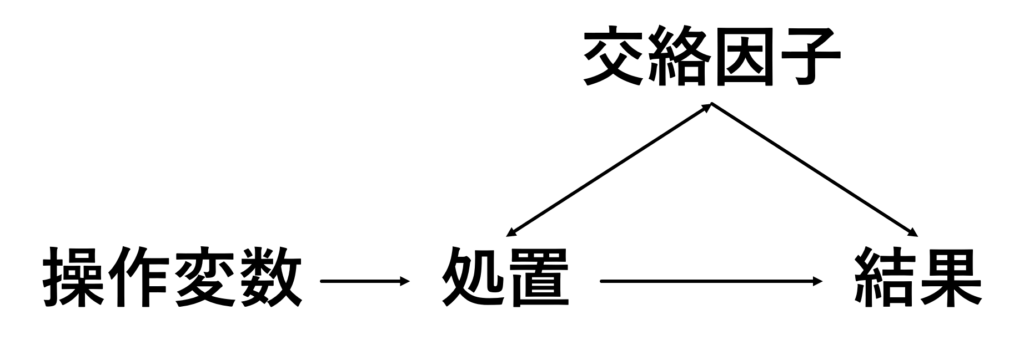
これはどういうことかというと,操作変数は処置の割り当てを左右するものだけど,結果には直接関連せず,処置の割り当てを通してのみ結果に影響を与えるようなものということです.
操作変数にはどのようなものがあるかというと,前述したRCTで「無作為化した処置の割り付け」がそれに該当します.無作為化において処置群に割り付けられた対象者の多くは処置を受けることが考えられますし,対照群に割り付けられた対象者の多くは処置を受けないことが考えられます.つまり無作為割り付けは処置の有無と強く関連しているということです.しかしどちらのグループに割り付けられたかが結果に影響を与えているのではなく,実際に処置をうけたかどうかが結果に影響を与えていることは想像に難くないですよね.つまり割り付け結果という操作変数は,結果に直接影響を与えていないわけです.
この図と説明をみると一見,結果と関係しない因子だから別に気にしなくても良いのでは?と思われるかもしれません.実はそのとおりで,通常の既存情報を用いた解析ではこの操作変数というものは考慮せずに解析を行います.むしろ考慮することによって処置効果の推定にネガティブな影響を与えることも示唆されています.ですが操作変数法では,この操作変数を利用することによって,全ての交絡因子の影響を取りはらってしまおうというぶっとんだ方法になります.
操作変数法のコンセプト
操作変数法では,この操作変数を利用して処置を受けるかどうかの選択を,
- 操作変数に依存する部分
- 操作変数以外に依存する部分
に分けてしまうことが肝になります.
例えば「私立中学校と公立中学校の学生間における成績の差」を検証する研究を例としてみます.今回は「私立中学校か公立中学校」が処置の位置にあたります(私立中学校へ通わせるという処置,と理解してもらうと分かりやすいかもしれません).また全国統一テスト等における成績を結果として考えます.また私立中学校と公立中学校に通う学生では,家庭の収入や学習塾等の学校以外での学習環境など様々な因子が異なるため,それらが「交絡因子」となることが考えられます.
この際,研究対象となる彼ら彼女らが中学校を受験する前に「私立中学校に入れば授業料が半額無料」になる権利をランダムに配布するという実験が行われていたとします.この半額免除の権利はもちろん私立大学に入るかどうかの選択には影響しますが,その後の学業成績には直接的に影響しない,つまり操作変数であると仮定します.
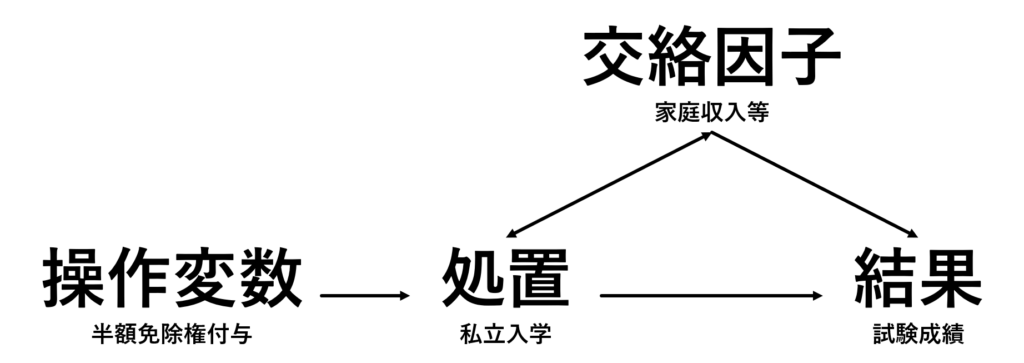
それでは今回の処置である「私立中学校入学の有無」の要素を二つに分けてみます.
- 操作変数に依存する部分 ⇒ 半額無料権が与えられるかどうか
- 操作変数以外に依存する部分 ⇒ 家庭の収入など
となりますね.
現実として研究対象者は皆さん私立・公立中学校のどちらかには所属しています.またその選択は,半額無料券をもらったから(操作変数に依る部分),また家庭収入やもともとの成績など諸事情(操作変数に依らない部分)を鑑みて決定されていることでしょう.それをまず区分しているのがこの段階です.

操作変数法では(1)に依存する部分のみの結果への影響を推定します.
具体的にどのようなステップを踏むのか,以下の図を見ながら説明していきます.
Step1:処置の有無を操作変数のみで予測する
実際の処置の有無(私立中学校への入学)は操作変数(半額免除権)以外の要素にも依存しているはずですが,このステップでは,処置の有無を操作変数のみで予測します.このように処置の有無を予測する際にその他の情報を一旦無視することによって,ここで計算した処置の有無の予測値というものは,操作変数以外の情報を除外したものということになります.次のステップでは,この「操作変数のみで予測された処置」の情報を利用して処置効果を推定していきます.
※数式については念のため記載しているだけですので読み飛ばしてもOKです.α1というのは操作変数が処置の有無に与える影響の大きさだと思ってください.

Step2:結果における処置予測値の効果を推定する
Step1で計算した「操作変数のみで予測された処置」が結果に与える影響(以下図中のβ1)を推定します.「操作変数のみで予測された処置」ではすでに交絡因子などの要素は除外されているので,もちろんここで推定した効果量(β1)にも交絡因子が影響してくることはありません.

前置きが長かった割に,やっていることはたったこれだけです.事前に操作変数以外の部分を除外することによって,交絡因子とかを帳消しにしてしまおうということですね.
これは二段階推定法というものでコンセプトの説明にはとても分かりやすいのですが,実際にこの方法で処置効果を推定すると,バイアスは防げますが,推定の精度の推測に問題が出てきます.この点については結構難しいところなので,細かい説明は避けて,解析の際にはその点も自動的に考慮できるようにしています.
EZRで操作変数法の解析手順
それでは操作変数法の解析にEZRを使ってチャレンジしてみましょう!ちなみに操作変数法のオプションは用意されていませんので,ここではRのスクリプトをコピペする形で実行してみましょう.パッケージのインストールなどが必要なので,初めて実施する場合はインターネット環境化で実行してくださいね.
今回は実際のデータを使うのではなく,本当に操作変数法が上手く機能しているのかを確認するために実験的に作成した以下のデータを利用しています.このデータは以下の手順1でダウンロード可能です.
| id | iv | cnf1 | cnf2 | treat | outcome |
| 1 | 1 | 0.077303 | 0.850043 | 0 | 67.46798 |
| 2 | 0 | -0.29687 | -0.92531 | 0 | 47.10014 |
| 3 | 0 | -1.18324 | 0.893581 | 1 | 76.63003 |
| 4 | 1 | 0.011293 | -0.94101 | 1 | 71.73025 |
| 5 | 1 | 0.991601 | 0.538952 | 0 | 74.70814 |
| 6 | 0 | 1.593967 | -0.18197 | 1 | 95.27978 |
| 7 | 1 | -1.37271 | 0.891768 | 1 | 73.85734 |
| 8 | 1 | -0.24961 | 1.329208 | 1 | 89.87022 |
| 9 | 1 | 1.159425 | -0.10347 | 1 | 89.48509 |
| 10 | 1 | -1.11422 | 0.615065 | 0 | 53.55731 |
- 対象症例1000名
- 操作変数(iv):処置の無作為割り当ては500:500にランダムに割り当てる
- 処置変数(treat):実際の処置の有無
- 交絡因子1(cnf1):測定されている交絡因子
- 交絡因子2(cnf2):測定されていない交絡因子(測定されていないだけで存在している)
- 結果変数(outcome):100点までの点数等の連続型変数
- 真の処置変数の結果変数における効果:+20点
今回のデータに対して操作変数法をあてはめた時に,真の処置変数の結果変数における効果である「20点」を正しく推定できればOKです!
また操作変数法と比較するため,一般的な線形回帰モデルを利用して,
- 交絡因子を考慮しない場合
- 測定されている交絡因子(cnf1)だけ考慮する場合
についても検討してみましょう.それでは実際の手順に入っていきます.
手順1.以下のデータセットをダウンロード
手順2.EZRを立ち上げて以下手順でデータを読み込む
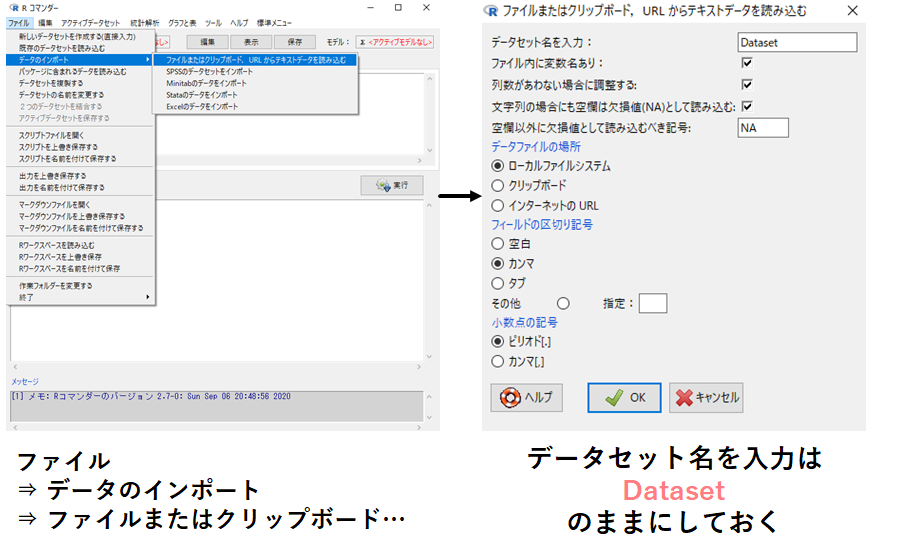
ファイル
⇒ データのインポート
⇒ ファイルまたはクリップボード,URLからデータを読み込む
⇒ データセット名をデフォルトのまま「Dataset」でOK
手順3.以下のコードをコピーしてEZR上「Rスクリプト」にペースト ⇒ 実行
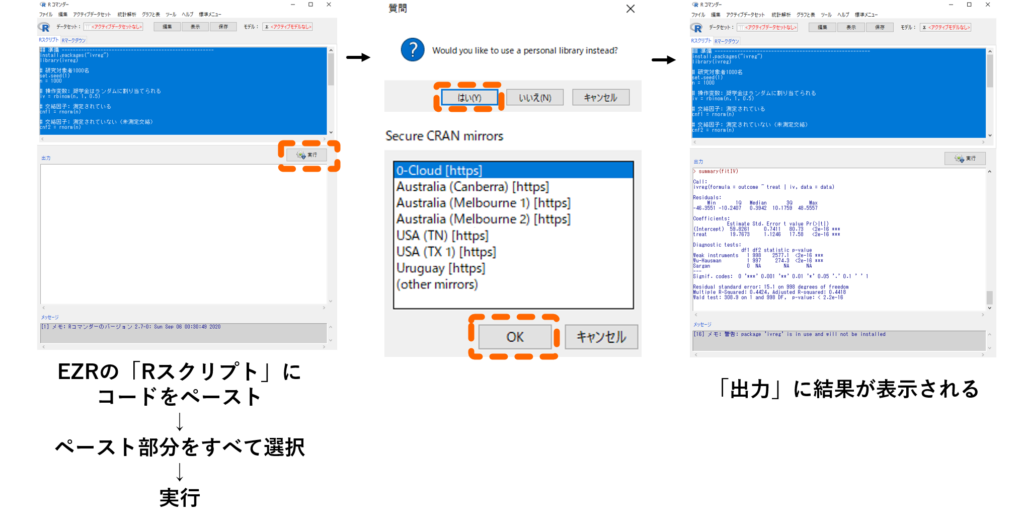
以下が解析用のRコードですので,以下をコピー&ペーストしてください.
## 準備 -------------------------------------------------------
install.packages("ivreg")
library(ivreg)
## 解析 -------------------------------------------------------
# 線形回帰モデル: 交絡因子を全く考慮しない場合
fit1 = glm(outcome ~ treat, Dataset, family = gaussian("identity"))
summary(fit1)
# 線形回帰モデル: 未測定交絡を考慮せずに解析した場合
fit2 = glm(outcome ~ treat + cnf1, Dataset, family = gaussian("identity"))
summary(fit2)
# 操作変数法
fitIV = ivreg(formula = outcome ~ treat | iv, data = Dataset)
summary(fitIV)それでは早速結果を見てみましょう!
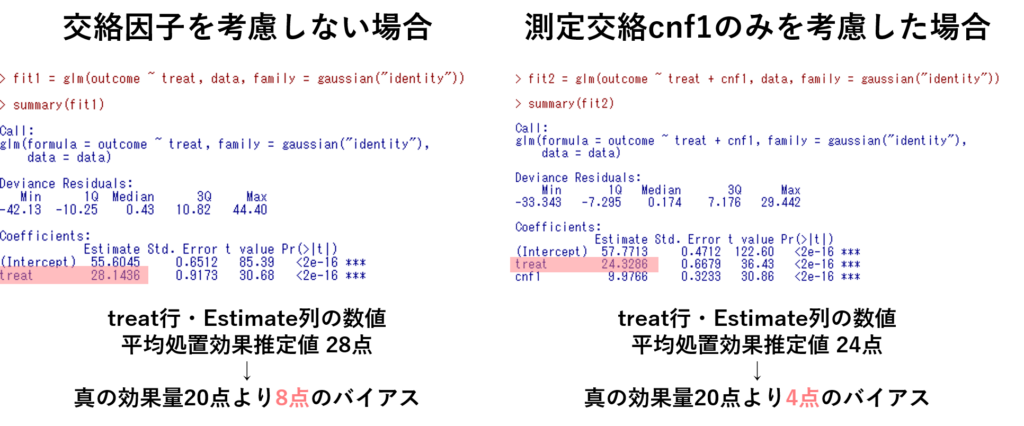
交絡因子を考慮しない場合では,以下の通り処置効果の推定値が20から大きく外れていることが分かります.つまり交絡によるバイアスが生じているということですね.また,測定されている交絡因子(cnf1)だけ考慮する場合も同様に,未測定な交絡を考慮していないことでバイアスが生じています.
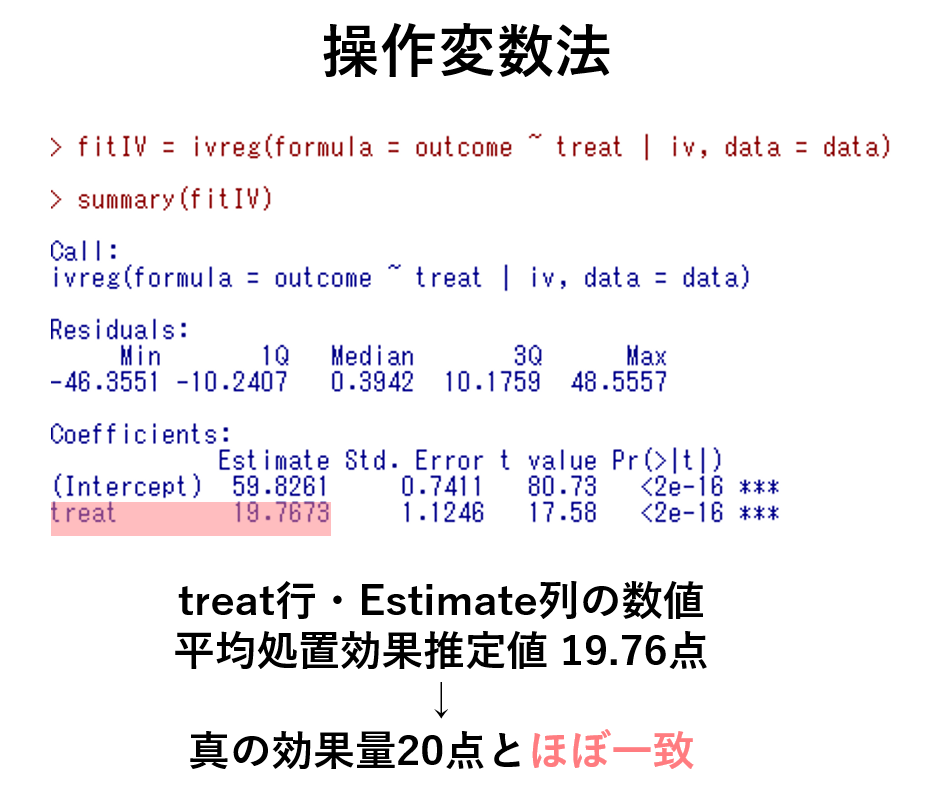
それでは操作変数法を用いた場合についてみてみましょう.操作変数法を用いた場合の平均処置効果推定値は真の処置効果である20にかなり近い値が得られていることが分かります.これで交絡因子が測定されていても,されていなくても,操作変数法を用いることで交絡によるバイアスが取り除くことができることを実感できたのではないでしょうか?
今回は実験的にデータを発生させて解析に利用しましたが,皆さんがご自身のデータに対して適用する際には,ご自身のデータをEZRのデータのインポートからデータを読み込んで,以下を実行してもらえれば実行できるはずです.それぞれの変数の名前は,データセット中の変数名と一致させてくださいね.
- データセット:Datasetと名前をつけてインポート(EZRではデフォルトでDatasetとなる)
- 操作変数:処置群に割り当て=1,対照群に割り当て=0
- 処置変数:処置有=1, 処置無=0
- 結果変数:連続型の変数
install.packages("ivreg")
library(ivreg)
fitIV = ivreg(formula = 結果変数 ~ 処置変数 | 操作変数, data = Dataset)
summary(fitIV)操作変数法の仮定
最後になりましたが,実は操作変数法が成立するためには非常に厳しい仮定がいくつか存在し,実際に解析を行う際には,皆さんのデータがその過程を満たしているかどうかの確認が必要になります.
- 仮定1:操作変数は処置変数と強く関連する
- 仮定2:操作変数は結果変数と直接関連しない(処置を介してのみ関連する)
- 仮定3:操作変数と結果変数の両方に関連する因子は存在しない
- 仮定4:操作変数と処置の関係は単調である
仮定1と仮定2は,上記で説明した操作変数の条件そのものなので大丈夫だと思います.ただ実際にはこの仮定を十分に満たすことができる要素というものはなかなか存在しません.専門家が口をそろえて操作変数と定義できるもので代表的なものといえば,RCTにおける無作為割り当てや,くじ引きのような,他の因子と完全に独立に決まるものくらいです.そのため多くの研究では操作変数法を用いていたとしても,それが本当に操作変数化どうかは怪しいとされています.
また仮定3は仮定2の拡張的なものというか,仮定2に含まれているようなものなのですが,操作変数は処置変数を介してのみ結果変数に影響を与えるため,処置変数と結果変数とに関係するような抜け道になる因子は存在しないよ,ということです.つまり処置変数と手をつないでいる友達は処置変数だけということですね.しかしこれらの仮定を証明することは難しく,仮定1についてはデータから判断できないことはありませんが,仮定2や3についてはデータからも判断できないため,ご自身の分野における専門性をもってロジカルに説明づける必要があります.これがまたとってもとっても大変で,操作変数法を適切に使うことが難しいと言われる所以でもあります.
さらに仮定4についてはちょっとややこしいのですが,4タイプのおばさまを想像してもらうと分かりやすいかなと思います(※おばさまとしているところには何の理由もありません.私自身に置き換えて想像しやすいというだけです…).
- タイプ1:生真面目おばさまタイプ「割り当てに従って処置を受けます」
- タイプ2:ミーハーおばさまタイプ「割り当てに関係なく処置は受けたいわ!」
- タイプ3:ネガティブおばさまタイプ「割り当てに関係なく処置は受けたくないわ!」
- タイプ4:逆張りおばさまタイプ「割り当てには絶対に従わないわ!反対を選ぶわ!」

操作変数法においてはタイプ4のような対象者がいないことを前提としています.この仮定については問題視される状況はあまりないのですが,一応そういう人が研究対象に入っていたらダメなんだな,程度に思っておいてください.またこれに関連したところでいうと,操作変数法で推定している平均処置効果は厳密にいうと「局所的平均処置効果(local average treatment effect: LATE)」というものを推定していることになります.実は操作変数法で推定している処置効果というのは割り当てどおりの処置をうけた対象者における効果のことを指しているんだな,ということも,何となく頭の片隅に置いておいてもらっても良いかもしれません(研究者にとっては結構大事なポイントなんですけどね…まずはさっくりと理解してもらって結構です).
まとめ
なんとなく操作変数とは何を目的として,どのようなことをしているのか掴むことができたでしょうか?なるべく必要なところはお話しつつ,解析のゴールまでを見据えならがら,難しいところは出来るだけ省いて説明をしてみました.
専門の書籍だけでは難しいよ,という方の理解の助けになれば幸いです.またこの記事を読んでゴールまでイメージできた後であれば,専門の書籍もすこしとっつきやすくなっているかもしれません.以下にとても有名な参考書籍の載せておりますので,是非参考にしてみてください.(今回の記事もこれらの書籍をよく参考にさせていただきました.)
おすすめの書籍
- (因果推論をRで学びたい方向け)統計的因果推論の理論と実装 (Wonderful R)
- (因果推論をPythonで学びたい方向け)つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門
- (因果推論の理論も学びたい方向け)調査観察データの統計科学: 因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)



コメント