記事の要約:EZRで傾向スコアマッチングの解析手順【図解】
この記事で学べること
- EZRによる傾向スコアの計算方法
- 傾向スコアを用いたマッチング方法
- マッチングされたデータの解析方法
この記事のまとめ
- 傾向スコアは背景情報から予測された処置をうける確率
- EZRを使えば簡単に傾向スコアの計算とマッチングができる
- マッチング後のデータの扱いには少し注意が必要
- EZRや因果推論に関する書籍は以下がおすすめ
- (因果推論をRで学びたい方向け)統計的因果推論の理論と実装 (Wonderful R)
- (因果推論をPythonで学びたい方向け)つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門
- (因果推論の理論も学びたい方向け)調査観察データの統計科学: 因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
傾向スコアとは
傾向スコアをざっくりと説明すると「背景情報から予測した処置確率」と説明できます.
例えば,一般的な臨床の現場では,血圧を下げるお薬が処方される確率は,もちろん元々の血圧が高い患者さんで高くなりますよね.当然医師の頭の中では,血圧以外にも年齢や他の臨床的情報など,さまざまな背景情報を考慮して,降圧薬の処方(処置)を行うかどうかを決めます.
傾向スコアはこの治療や処置が行われる確率を,手元に得られている患者さんの背景情報などから予測したものになります.実際には多変量のロジスティック回帰モデルなどを用いて,複数の背景情報を同時に考慮した予測確率を計算することになります.
傾向スコアを使うメリット
例えば降圧薬の処置効果を知りたいとなれば,処置グループと非処置グループ同士でその後1年間における心臓病の発生割合を比べたりしますよね.しかし日常の臨床情報をそのまま使うような,処置をランダムに割り付けてない研究では,必ず交絡という現象が問題になります.交絡についてはこちらの記事で詳しく図解していますが,簡単に要約すると「処置グループと非処置グループで背景情報が異なるとフェアに比べられない」というものだと思ってください.
例えば臨床現場で医師はより具合の悪い患者さんに降圧薬処方をしていたとします.もちろんこの患者さんたちはもともと具合が悪いので,将来的に心臓病が発生するリスクは高い人たちです.このように,処置グループには非処置グループより具合の悪い人が多くいるようなデータを使って,その後の心臓病のリスクを比べてしまうと,どうしても処置グループで不利な結果が出やすくなってしまいますよね.つまりもともとの背景情報の不均衡によって,本当に知りたい処置の効果がわからなくなってしまうという問題が生じます.
ここで傾向スコアに話を戻すと,上記の通り,傾向スコアは複数の背景情報を確率として表現したものであり,患者さんの背景情報を統合した情報であると考えることができます.つまり「同じような傾向スコアをもつ患者さん同士は,同じような背景情報をもつだろう」と考えることができます.
処置グループと非処置グループに同じような傾向スコアをもつ患者さんが同じくらいの割合で存在すれば,処置グループと非処置グループの背景情報に差がなくなるのではないか?と考えられます.グループ間の背景に差がなくなるのであれば,上記のような交絡の問題は除去できそうですよね.これがデータ解析において傾向スコアを利用する一般的なメリットになります.
傾向スコアを用いてグループ間の背景情報の差を小さくする方法としては,マッチング,重み付け,層別化などがよく利用されます.この記事ではまずEZRによる傾向スコアを用いたマッチングの方法について解説していきます.
傾向スコアマッチングでは何をしているのか?
傾向スコアマッチングはその名前のとおり,類似した傾向スコアをもつ対象者同士をマッチングして,解析用データを作る方法です.
以下の例では,治療などの処置をうけたグループには,もともと具合の悪い(リスクの高い)対象者が多く存在していることが分かります.この状態で処置グループと非処置グループを比べてしまうと,上記で説明した通り,フェアな比較はできませんよね.
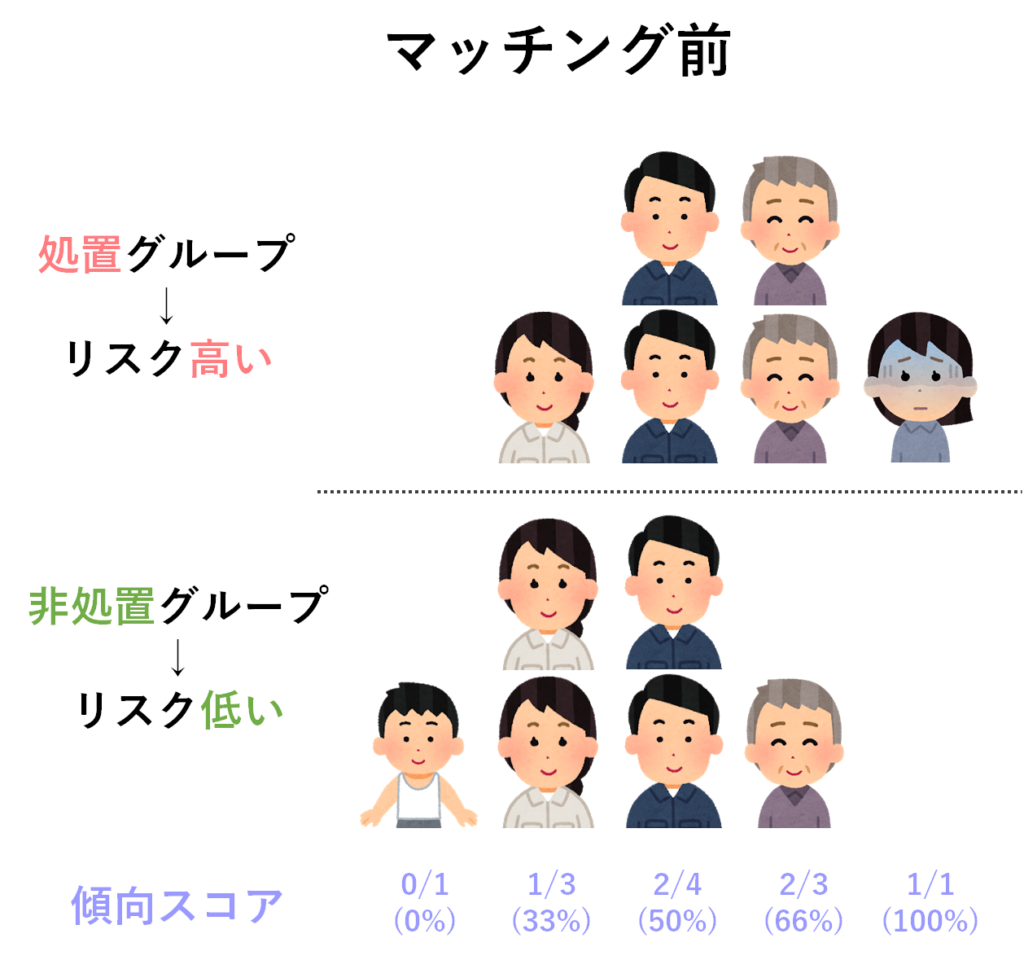
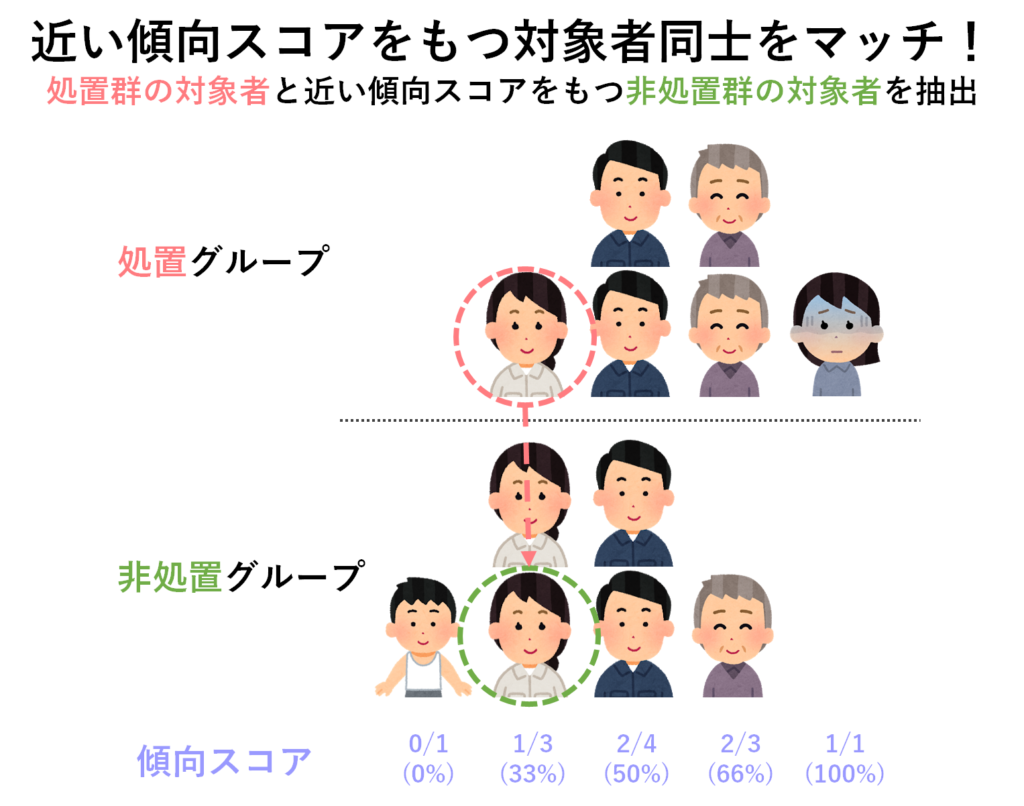
そこで傾向スコアマッチングでは,両グループから類似した傾向スコアをもつ対象者同士を抽出してきます(厳密には,処置群の対象者の傾向スコアを基準に,非処置群からマッチ相手を探します).すると当然,両グループには類似した傾向スコアをもつ,類似した状態の患者さんが同じ(割合)だけが含まれるようになりましたね.ちなみにここではマッチ相手がうまく見つからなかった対象者は除外する方法を使っています.
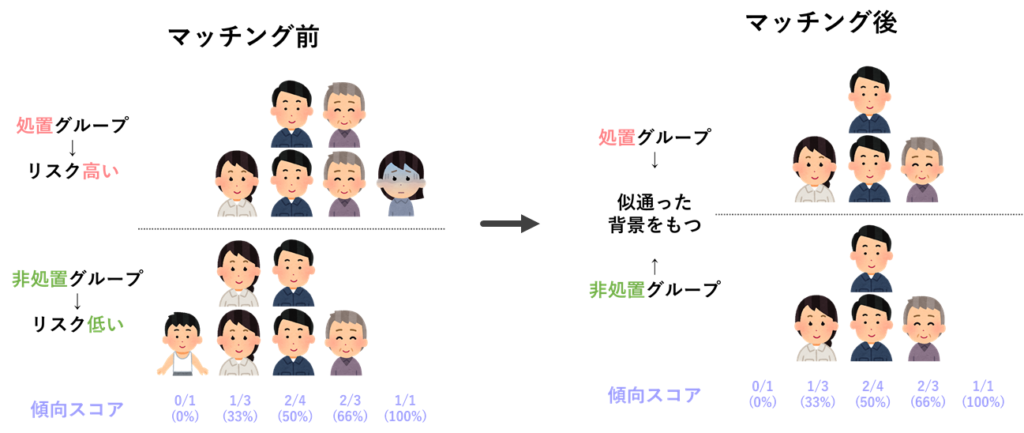
マッチングの前後で見比べてみると,グループ間の対象者の状態に差がなくなったことが良くわかります.この状態であれば,誰がみても,もともとのグループ間の特徴が似通っていることが分かります.傾向スコアマッチングが医学研究でも良く利用される要因のひとつには,この「分かり易さ」があるように思います.
このように傾向スコアを使ったマッチングは,年齢や性別,その他既往歴など,対象者の状態をひとつひとつ確認しなくても,傾向スコアだけをマッチングすれば,グループ間の対象者の状態を揃えることができる非常に便利な方法であることが分かります.
事前準備:データのダウンロードと読み込み
それでは早速データセットを読みこんで傾向スコアマッチングを行ってみましょう.
データセットは練習用のCSVデータを準備しましたので,手元にちょうどよいデータがなければ,これらをダウンロードしてご利用ください.
| id | iv | cnf1 | cnf2 | ・・・ | outcome_num | outcome_skew | outcome_ord | time |
| 1 | 0 | 0.14 | 0 | ・・・ | 200.9 | 0 | 1 | 0.04 |
| 2 | 0 | 0.41 | 1 | ・・・ | 160.37 | 0 | 1 | 0.11 |
| 3 | 1 | -0.07 | 0 | ・・・ | 461.07 | 158.34 | 3 | 0.08 |
| 4 | 1 | -0.25 | 0 | ・・・ | 363.76 | 76.03 | 2 | 0.02 |
| 5 | 0 | 0.7 | 0 | ・・・ | 290.58 | 0 | 1 | 0.02 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 496 | 0 | -1.35 | 1 | ・・・ | 227.81 | 0 | 1 | 0.11 |
| 497 | 0 | 1.03 | 0 | ・・・ | 170.44 | 0 | 1 | 0.17 |
| 498 | 1 | -0.81 | 0 | ・・・ | 326.61 | 44.92 | 2 | 0.2 |
| 499 | 1 | 1.8 | 0 | ・・・ | 256.07 | 0 | 1 | 0.13 |
| 500 | 0 | 1.77 | 0 | ・・・ | 197.09 | 0 | 1 | 0 |
※11人目以降は省略
準備1.参考データ(CSV)をダウンロード
※後ほどEZRで読み込みたいデータの場所を指定する必要があるため,デスクトップなど自分が分かりやすい場所に保存しておくことをおすすめします!
準備2.EZRを起動 ⇒ CSVファイルの読み込み
CSV・Excelファイルのpythonにおける読みこみ方は,以下で詳しく説明していますので,参考にしてみてください.今回はデータセット名はデフォルトのまま Dataset と名前をつけて読みこんでいます.
傾向スコアマッチングの手順
傾向スコアマッチングを行う手順は大きく4つに別れます.
- 傾向スコアを推定する
- 傾向スコアを使ってマッチングする
- マッチング前後で背景情報のバランスを確認する
- マッチングされたデータでグループ間の比較を行う
1.傾向スコアを推定する
まずは傾向スコアを推定してみましょう.基本的に傾向スコアはロジスティック回帰モデルを用いて推定します.もちろん他にも色々な方法があります.最近(?)では機械学習をつかって推定する方法もよく使われます.今回はロジスティック回帰モデルを使って推定してみましょう.
今回は処置変数である treat_bin (1:処置あり, 0:処置なし) に関する傾向スコア(treat_bin=1となる予測確率)を背景情報である cnf1 と cnf2 から計算してみます.
- 名義変数の解析
- 二値変数に対する多変量解析(ロジスティック回帰)
- 目的変数 欄にカーソルをあてて処置変数 treat_bin をダブルクリック(※1)
- 説明変数 欄にカーソルをあてて交絡因子 cnf1 と cnf2 をそれぞれダブルクリック(※2)
- □傾向スコア変数を自動作成する にチェックを入れる
- OK
※1.画面を開いた時点ですでに「目的変数」欄にカーソルが当たっているはずです
※2.treat_bin をダブルクリックしたら自動的に「説明変数」欄にカーソルが移動します
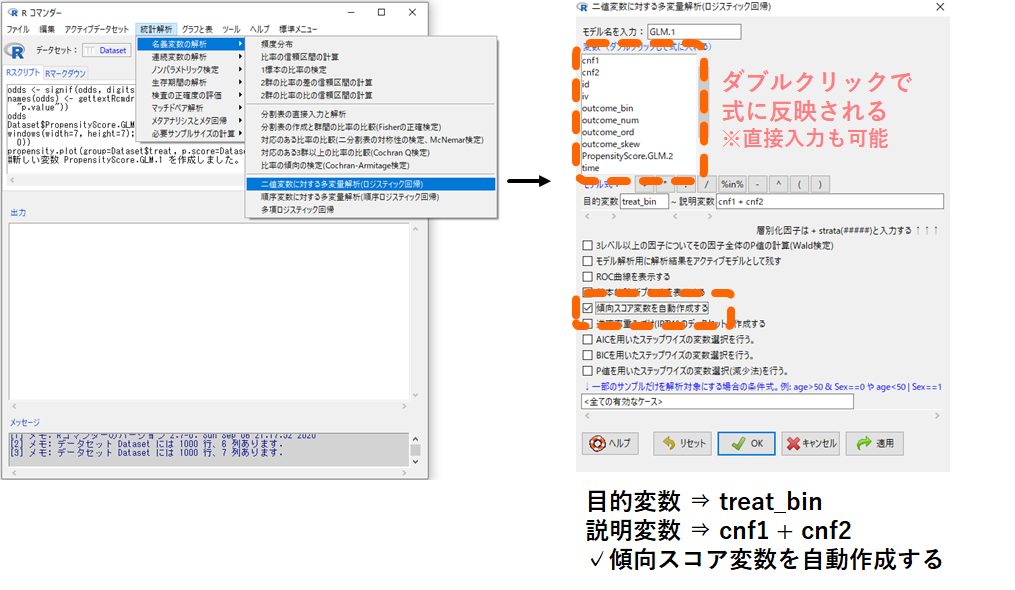
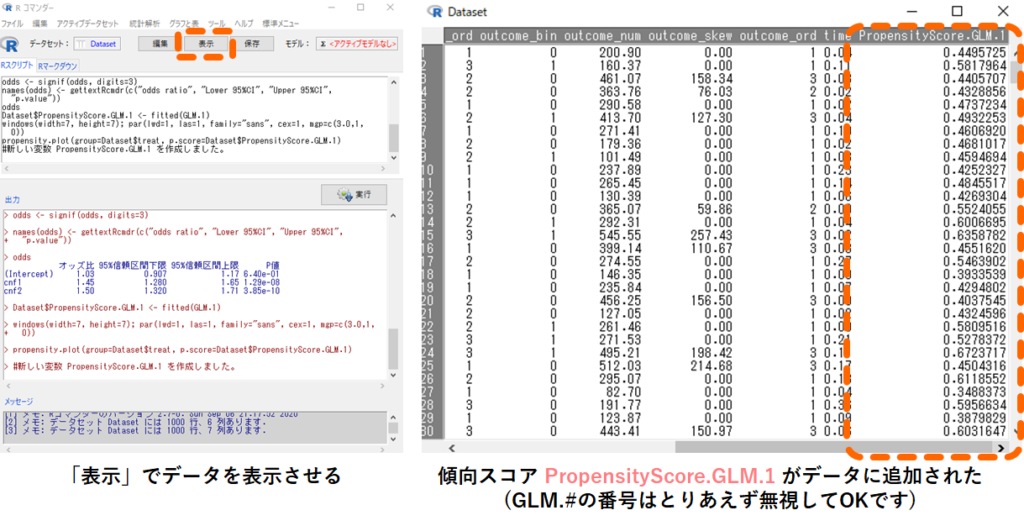
これで各対象者について,背景情報 cnf1 と cnf2 から計算された傾向スコアがデータDatasetに保存されているはずです.早速データの中身を以下手順で見てみましょう.データの一番右端に「PropensityScore.GLM.1」という新しい変数ができていますね.これがcnf1とcnf2から予測した各研究対象者において処置が行われる確率であり,傾向スコアになります.
※GLM.#の番号は何回目に推定を行ったものかを示しているだけなので,気にしなくても大丈夫です.
2.傾向スコアを使ってマッチングする
傾向スコアが推定できたので,以下の手順で早速マッチングを行ってみましょう.傾向スコアマッチングも種類は色々とあるのですが,今回は処置グループと非処置グループを1:1でマッチングしてみましょう.
- 統計解析
- マッチドペア解析
- マッチさせたコントロールの抽出
- [比較する群の変数] treat_bin, [マッチさせる変数] PropensityScore.GLM.#
- OK
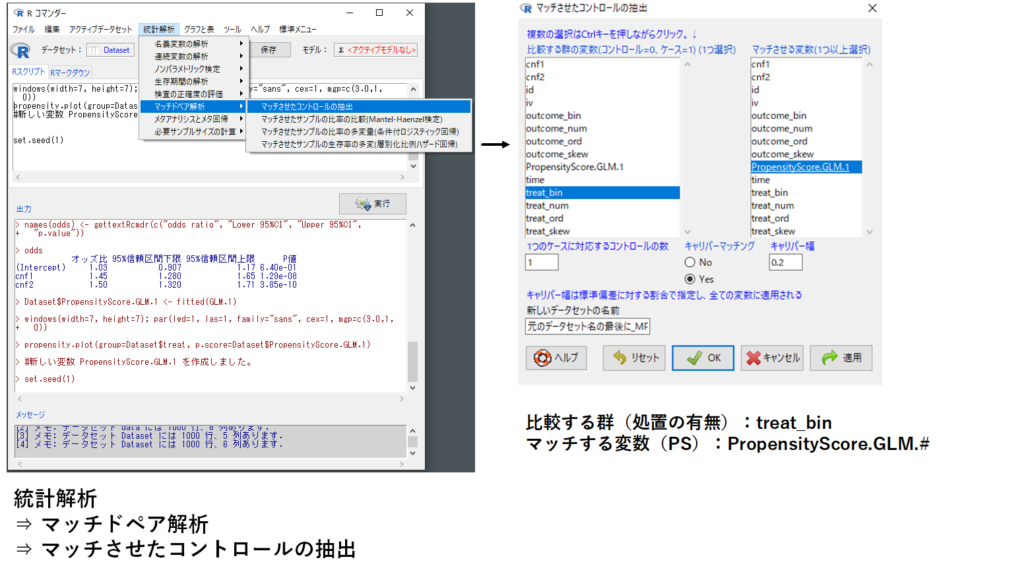
これでマッチングのステップは完了です.マッチングされたデータセットは,マッチング前のデータセット名(Dataset)の末尾に _MP(Matched Pair)が追記された名前 Dataset_MP で保存されています.今回のマッチングでは424名の対象者のデータが抽出されました.
※ マッチングの仕方ひとつをとっても色々とありますが,今回は,Caliper (=0.2) を利用したマッチングというものを利用しています.Caliperというのは「マッチ相手を探す幅」と解釈してください.つまりどれくらい傾向スコアが離れた相手までならマッチングしますか?という幅を指定しています.EZRで Caliper = 0.2 として設定した場合には「処置群の対象者にマッチする非処置群のマッチ相手を探すときに,処置群の対象者の傾向スコア ± 傾向スコアの標準偏差×0.2 の範囲までで検索する」ということになります.あまり難しいことは考えずに「Caliperを狭くするとより近い傾向スコアを持つ者同士だけがマッチングされるようになる」と考えておけばOKです.このCaliperは一般的に0.2程度が使われますが,当然もっとグループ間の背景を綺麗に揃えたければ,0.2よりも狭い値に設定しても問題ありません(その代わりうまくマッチングされない可能性もでてきますので,マッチング後にのこる対象者数が少なくなってしまうリスクはあります).
※ EZRではマッチングを傾向スコアで行っていますが,実際の研究では傾向スコアではなく「対数化オッズ(logit)」という傾向スコアを数値変換したものを利用することが一般的です.これにも理由は色々とあるのですが,その方がマッチングが上手くいくのだ,程度に考えておいてください.(傾向スコアそのものでマッチングをしては絶対にいけない,という訳ではありません.)
3.マッチング前後で背景情報のバランスを確認する
それではマッチング前後で,背景情報が揃ったかどうかを確認してみましょう.背景の揃い方の確認する方法も色々とありますが,今回は背景表の計算時に Standardized Mean Difference (SMD) を使ってみます.SMDは0に近いほどグループ間の背景情報の差が小さいと考えることができます.
以下の2つを確認して,マッチング前後でSMDが小さくなっていることを確認してみましょう.
- Dataset(マッチング前)を使った背景表
- Dataset_MP(マッチング後)を使った背景表
実はEZRではマッチング後のデータだけでなく,マッチング前のデータなど,ここまでに読みこんだデータが保管されています.解析においてどのデータを使うかは データセット ボタンをクリックすると選択できるようになります.
- データセットに「Dataset」あるいは「Dataset_MP」を選択
- グラフと表
- サンプルの背景データのサマリー表の出力
- [群別する変数] treat_bin, [カテゴリー変数] cnf2, [連続変数(正規分布)] cnf1
- [カテゴリー変数の検定方法] 独立性のカイ二乗検定, [標準化差を表示する] Yes
- OK
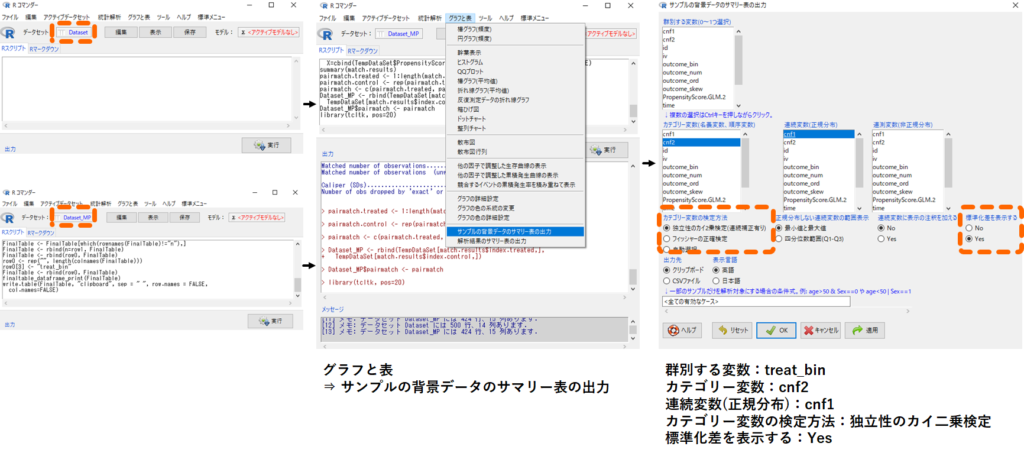
作成した結果は以下のようになりました.マッチング前はSMDが0.2付近ですが,マッチング後は非常に小さくなっていますね.実際にそれぞれの背景情報の値をみてみても,マッチング後は,カテゴリー変数であるcnf2については1となる対象者の割合が両群共に29.2%で揃っていますね.また連続変数であるcnf1については平均値が-0.1付近で揃っています.うまくマッチングできていますね!これでグループ間での背景情報の不均衡を取り除くことができました!

4.マッチングされたデータでグループ間の比較を行
マッチングによって背景も揃えることができたので,やっとこれでグループ間の結果変数をフェアに比べることができそうですね.次のステップでは,グループ間で結果変数を比べてみます.2つのグループ間で結果変数を比較する解析手法には主に以下のような手法が使われます.
| 結果変数の尺度 | 一般的な仮説検定手法 | 回帰モデルで実行する場合 |
| 連続 | スチューデントのt検定(正規分布) マンホイットニ―のU検定(非正規分布) |
線形回帰モデル |
| 二値 | カイ二乗検定(対象者数≧40) フィッシャーの正確検定 |
ロジスティック回帰モデル |
| 初発イベントまでの時間 | ログランク検定 | Cox比例ハザード回帰モデル |
今回の例では結果変数である outcome_num は連続変数であり,このデータは各グループごとに正規分布にも従っています.そのため今回は スチューデントのt検定を行ってみましょう.
- 統計解析
- 連続変数の解析
- 2群間の平均値の比較(t検定)
- [目的変数] outcome_num, [比較する群] treat_bin
- OK
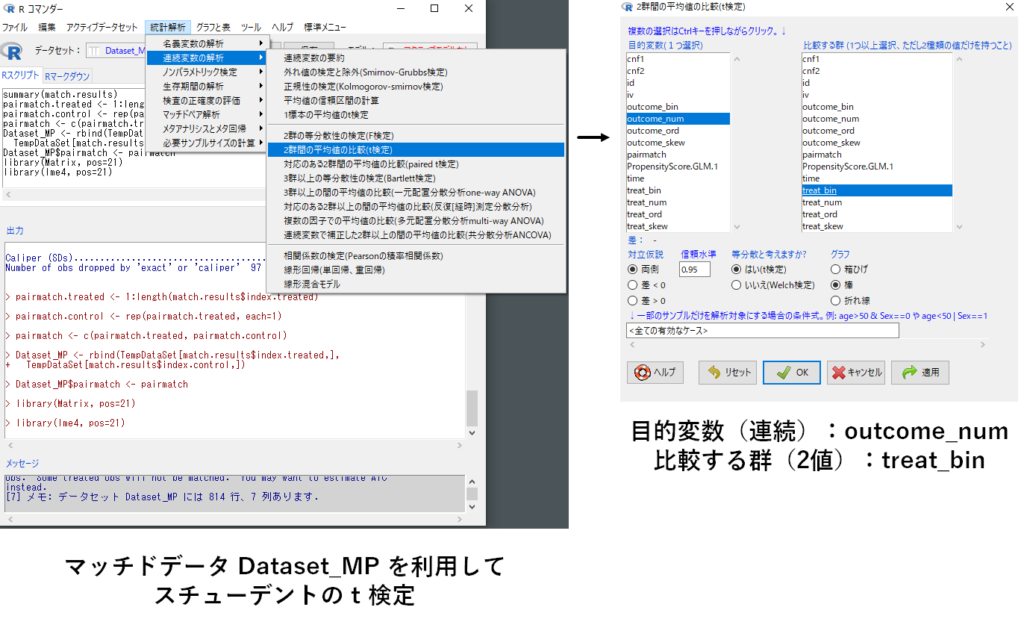
実行すると,以下のような結果が得られます.
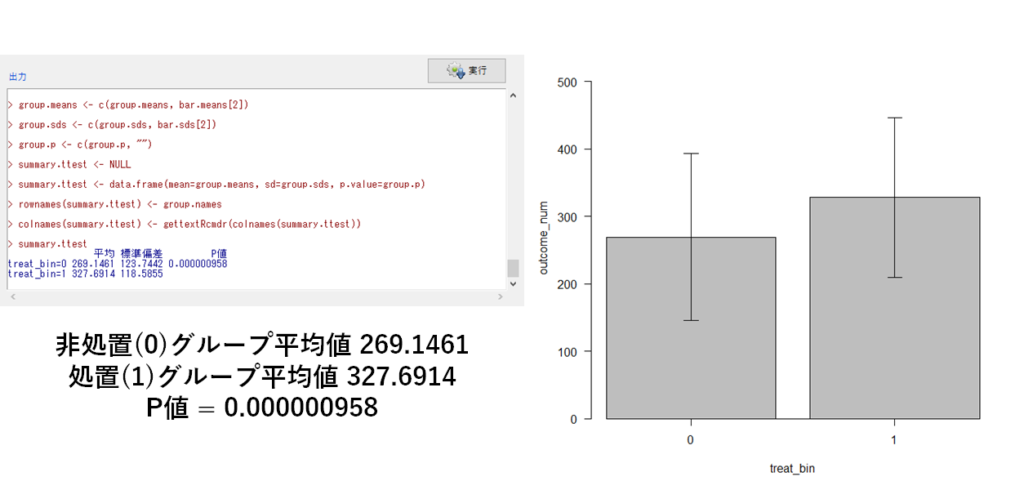
今回はグループ間で outcome_num を比較した結果,処置群では平均値が約60くらい高くなることが分かります.マッチングのステップで背景情報である cnf1 や cnf2 の状態はグループ間で揃えることができていますので,それらの背景情報の不均衡によるバイアス,つまり交絡は起こっていない結果と考えることが出来そうです.
※ 当然ですが,一般的な研究においては,かなり多くの因子が交絡因子となっている可能性があり,それらすべてを傾向スコア推定時に考慮しなければ,交絡を完全に取り除くことはできません.また理論的には全ての交絡因子が考慮されていることが理想なのですが,実際にそのようなことが叶う訳もなく,実際にはより”上手に”交絡を生じさせ得る因子を選んで考慮する必要があります.(上手にの定義も色々とあります…)
※ 上記で紹介した方法はマッチングされた対象者同士の相関等を考慮せずに,グループ間の比較を行っています.通常このような方法では検出力が低下する(表面的な表現としてはp値が大きくなりやすい)という問題が生じます.このマッチングされた対象者同士の相関をどう考慮するべきかについても色々と議論があり,すこし難しい手法を使う必要があるため,今回は簡単な方法を紹介しています.この簡単な方法は「効果がない」と保守的な結果をだしてしまう可能性はありますが,過剰に「効果がある」と言ってしまう間違いは起こりにくいため,国際的な専門雑誌でも許容されていることが一般的です.(このあたりについても以下の論文が非常に勉強になります)
Matching methods for causal inference: A review and a look forward (Elizabeth A. StuartStat Sci. Author manuscript; available in PMC 2010 Sep 22.Published in final edited form as: Stat Sci. 2010 Feb 1; 25(1): 1–21. doi: 10.1214/09-STS313PMCID: PMC2943670)
まとめ
今回はEZRを用いた傾向スコアマッチングの解析手法に関する一連の流れについて紹介しました.EZRを使えば難しい操作なく傾向スコアの推定からマッチング,グループ間での背景情報のバランス確認が可能です.
またEZRで使える因果推論系の機能も日々アップデートされているので,今後も楽しみですね.
EZR開発者の先生が出されている書籍や,因果推論についてもっと専門的なところまで勉強したいという方にお勧めの書籍も以下に紹介しておきます.
- (因果推論をRで学びたい方向け)統計的因果推論の理論と実装 (Wonderful R)
- (因果推論をPythonで学びたい方向け)つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門
- (因果推論の理論も学びたい方向け)調査観察データの統計科学: 因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)




コメント