記事の要約:多変量線形回帰モデルと図のつくり方【図解】
この記事で学べること
- 多変量の線形回帰モデルとは?
- statmodelsライブラリによる多変量線形回帰モデルを用いた解析方法
- 多変量線形回帰モデルの結果の図示化
この記事のまとめ
- 多変量線形回帰モデルは複数の因子から連続尺度の結果変数を説明変数で説明(予測)する
- statmodelsを使えば結果の表示まで簡単にできる
- 特定の因子の影響力を図示化するにはちょっとコツが必要
- pythonの基本を学ぶスクールは以下がおススメ
Code camp
Teach academy
多変量の線形回帰モデルとは?
線形回帰モデルとは,連続尺度の結果変数を説明変数で説明(予測)する統計モデルのことです.こちらの記事で線形回帰モデルの基本について紹介していますが,説明変数が複数ある場合には多変量線形回帰モデルと呼んだりします(重回帰モデルと呼ばれることも).以下の式で表すように,複数の説明変数と1つの結果変数の関係性を表現することができます.
$$ Y = alpha + beta_1 X_1 + beta_2 X_2 + varepsilon $$
上記では2つの説明変数X1, X2と,結果変数Yとの関係をそれぞれβ1, β2で表現しています.ここでは数学的に細かいお話は省きますが,このβは「説明変数Xが1増加したときに結果変数Yがβだけ変化する」という風に解釈することができます.専門用語では「回帰係数」と呼びます.
説明変数がひとつだけの時はここまでの理解で良かったのですが,多変量モデルでは複数の説明変数を同時に考慮しているため,少しだけ解釈に注意が必要です.X1とX2を同時に考慮している場合には,X1がYに及ぼす影響と,X2がYに及ぼす影響を独立に考えることができます.つまりX1の影響力を示すβ1の値というのはX2の値には依存しないよ,と考えているということです.
…と言われても,よくわからないですよね(笑) 例を出して考えてみましょう.
例えばあるクラスで 算数のテスト成績(Y)に対する,性別(X1:女性0/男性1)の影響を調べるためにデータをとってみたとします.これを単変量の線形回帰モデルで推測すると以下のような式を使います.
$$ 算数のテスト成績 = alpha + 10 性別 + varepsilon $$
この結果は「男性(1)は女性(0)に比べて,テストの成績が平均的に10点低い」と考えることができます(説明変数である性別が1だけ増えたときに結果変数である成績が10点下がる).非常に分かり易い結果ですが,ちょっと意地悪なコメントをしてみましょう.
「このクラスでは確かに女子の方が平均点が10点高くいかもしれないけど,同時に女子は男子より1時間多く勉強してるよ.だから性別による差ではなくて,勉強時間によって差が出たんじゃないの?」
よくありそうな話ですよね.私たちが普段頭の中では普通に考えていることですが,上記の単変量の線形回帰モデルではそのあたりが考慮できていないのではないか?ということです.ここで複数の因子を同時に考慮できる多変量線形回帰分析の出番になります.
上記の性別のみを考慮していたモデルに,勉強時間(X2:時間)を加えた多変量線形回帰モデルを考えてみると,性別と勉強時間について,以下のような影響力を持っていることが推定されました.
$$ 算数のテスト成績 = alpha + 0 性別 + 10 勉強時間 + varepsilon $$
ここでは,勉強時間の回帰係数推定値が10であり「勉強時間が1時間の増えると,テストの成績が平均的に10点上がる」という結果が得られました.しかし同時に,性別の回帰係数が0となり「性別によってテストの成績が平均的に変わらない」という結果になりました.
この結果をみると,先ほどの単変量の回帰モデルでは性別によって成績に差があると読み取れましたが,その性別の差だと思っていたものは,実は勉強時間の影響によって生じるものだったということが分かります.つまり本来は性別はテストの点数に関連しないのに,勉強時間が男女間で異なることによって,性別とテストの点数が見かけ上関連しているように見えていただけだということです(これを専門用語では交絡と呼びます).
多変量の回帰モデルでは,このように複数の説明変数間の関係性を考慮した上で,どの説明変数が結果変数に大きな重み(影響力)をもっているのかを推測することができ,上記のような見かけ上の関連性を取り除いた解析を行うことができるというメリットがあります.(当然,性別と勉強時間以外にもテストの点数に影響を及ぼすものは沢山ありますので,非常に多くの因子が交絡因子となり得ます.どのような因子を多変量モデルで考慮すべきか等は,また別の記事で紹介したいと思います.)
また,今回多変量回帰モデルで得られた「勉強時間が1時間のびると,テストの成績が平均的に10点上がる」という勉強時間の影響は,性別に関係ないものである,つまり女の子でも男の子でも勉強時間を1時間増やすとテストの成績は10点くらい伸びるだろう,と考えられます.つまりもう「勉強時間による映鏡じゃなくて,性別による差なんじゃないの?」などという議論は出てこないわけです.
同様に「男性(1)は女性(0)に比べて,テストの成績が平均的に差がない」という性別による影響についても,勉強時間とは関係のないものである,つまり1時間でも5時間でも同じ勉強時間であれば,男女間では平均的に差はないだろう,と考えられます.
多変量回帰モデルではこのように,同時に考慮した説明変数の影響を無視したうえで,関心のある因子の効果や影響を推定することができます.
…とまあ色々とお話をしましたが,何はともあれ,Pythonで多変量の線形回帰分析とその結果の図示化に進んでいきましょう!
事前準備:データのダウンロード
それでは早速データセットを読みこんで解析していきましょう.
python,Anaconda3をインストールした際に使えるようになるSpyderという環境で操作します.Python単体でも同様のスクリプトで実行可能ですが,Spyderにはいろいろな補助機能があるため,こちらを使っていきましょう.
データセットは練習用のCSVデータを準備しましたので,手元にちょうどよいデータがなければ,これらをダウンロードしてご利用ください.
| id | iv | cnf1 | cnf2 | ・・・ | outcome_num | outcome_skew | outcome_ord | time |
| 1 | 0 | 0.14 | 0 | ・・・ | 200.9 | 0 | 1 | 0.04 |
| 2 | 0 | 0.41 | 1 | ・・・ | 160.37 | 0 | 1 | 0.11 |
| 3 | 1 | -0.07 | 0 | ・・・ | 461.07 | 158.34 | 3 | 0.08 |
| 4 | 1 | -0.25 | 0 | ・・・ | 363.76 | 76.03 | 2 | 0.02 |
| 5 | 0 | 0.7 | 0 | ・・・ | 290.58 | 0 | 1 | 0.02 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 496 | 0 | -1.35 | 1 | ・・・ | 227.81 | 0 | 1 | 0.11 |
| 497 | 0 | 1.03 | 0 | ・・・ | 170.44 | 0 | 1 | 0.17 |
| 498 | 1 | -0.81 | 0 | ・・・ | 326.61 | 44.92 | 2 | 0.2 |
| 499 | 1 | 1.8 | 0 | ・・・ | 256.07 | 0 | 1 | 0.13 |
| 500 | 0 | 1.77 | 0 | ・・・ | 197.09 | 0 | 1 | 0 |
※11人目以降は省略
準備1.参考データ(CSV)をダウンロード
※後ほどSpyder上で読み込みたいデータの場所を指定する必要があるため,デスクトップなど自分が分かりやすい場所に保存しておくことをおすすめします!
準備2.Spyderを起動 ⇒ 新規ファイルを作成 ⇒ CSVファイルの読み込み
CSV・Excelファイルのpythonにおける読みこみ方は,以下で詳しく説明していますので,参考にしてみてください.今回はデータセットを df と名前をつけて読みこんでいます.
# pandasライブラリをpdを名前をつけて使える状態にする
import pandas as pd
# pdに含まれるread_csvというメゾッドを使ってデータを読みこみdfとして保存
# データの格納場所は適宜修正してください
df = pd.read_csv("/Users/USERNAME/Desktop/robustwife/robustwife_all.csv", encoding="utf-8") statmodelsライブラリで多変量の線形回帰分析
線形回帰モデルが扱えるライブラリは沢山ありますが,解析から結果のまとめまでが全て簡単に行えるstatmodelsライブラリを今回は紹介します(公式).statmodelsライブラリは,回帰モデル全般を扱うことができるライブラリで,実際の解析でも非常に重宝しています.
多変量の線形回帰分析をpythonで実行する
statmodelsライブラリで線形回帰分析を行う際には ols 関数を使います.ols関数においては結果変数と説明変数をそれぞれ指定する必要がありますが,その方法は2通りあります.1の方法がより直感的かつ,変数を抽出するステップなどを省略できますので,今回は1の方法を採用します.
- “結果変数 ~ 説明変数1 + 説明変数2” という式 + 利用するデータセット名 を入力する
- 結果変数と説明変数データフレームをそれぞれデータセットから抽出してから入力する
今回は結果変数である outcome_num と説明変数である treat_num の関係について,cnf1, cnf2 という他2つの説明変数の影響を考慮した上で推定してみます.
# statsmodelsライブラリを使える状態にする
import statsmodels.formula.api as smf
# モデルの構築ols(目的変数Y~説明変数X)
results = smf.ols("outcome_num ~ treat_num + cnf1 + cnf2", data=df).fit()
# 出力
results.summary()
上記を実行してもらえれば,線形回帰モデルの結果が results に保存されます.resultsの内容を要約して表示するために result.summary() と入力しています.結果がひとめに分かるようになりましたね.
今回は treat_num という説明変数が outcome_num という結果変数にどの程度提供を与えていたのかを検討する際には,treat_num 行の coef 列を見てください.ここに記載されている20.93という数値が treat_num の回帰係数(つまりこれが回帰係数β = coefficient)の推定値です.つまり「treat_num が1上昇したときにoutcome_numが20.93上昇する」という風に理解できます.
また今回は多変量モデルということで,cnf1とcnf2という説明変数についても同時にそれらの影響を推定できていることがわかりますね.
95%信頼区間やp値のざっくりとした解釈については,単変量の線形回帰モデルの記事で紹介していますので,必要に応じて参考にしてみてください.
線形回帰分析で推定した結果を図で俯瞰する
上記までの結果のように,数字だけで示されても,どのような結果が得られているのかいまいち実感できない…という方もいるかと思います.これは研究者でも同じで,同じ結果であっても,図示化してあげるだけで理解度はぐっと高まります.ここでは上記で得られた結果を図示化する方法について説明します.
線形回帰モデルの結果を図示化は seaborn というライブラリを使って簡単に実行できたのですが,多変量の場合には少し工夫が必要です.特にpythonを実務で使いたいという方が躓くことの多いポイントの1つかなと思います.
seabornライブラリで2変数間の線形な関係を図示する際には jointplot 関数を使います.jointplot関数において結果変数yと説明変数xをそれぞれ指定すると,その2変数間の関係を表示してくれます.
# seabornライブラリを使える状態にする
import seaborn as sns
# outcome_numとtreat_numの線形な関係を可視化する
sns.jointplot(x="treat_num", y="outcome_num", data = df, kind = "reg", scatter = False)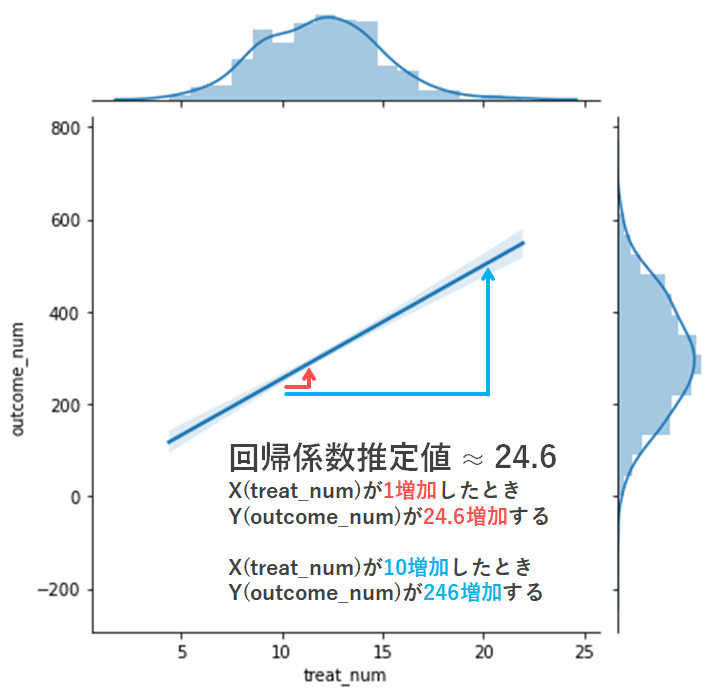
いかがでしょうか?図をみると2つの変数の関係性がより良く把握できそうですね.また上記で説明した回帰係数推定値の解釈についても,図にあわせて追記してみましたので,参考にしてみてください.
線形回帰モデルで予測された結果変数の値を表示
線形回帰モデルについて,XのYにおける影響力(あるいは両者の関係性)を知りたい場合は上記で説明した回帰係数推定値を確認すればOKですが,モデルによって結果変数Yの値を予測したいという場合もあります.モデルによって得られた予測値を取得する場合には,以下のコードを実行してください.ここでは予測値と一緒に,推定の誤差範囲を示す指標である95%信頼区間(lower=下限値,upper=上限値)も抽出しています.
# Yの予測値を取得
pred = results.get_prediction()
frame = pred.summary_frame(alpha=0.05)
frame["mean"]
frame["mean_ci_lower"]
frame["mean_ci_upper"]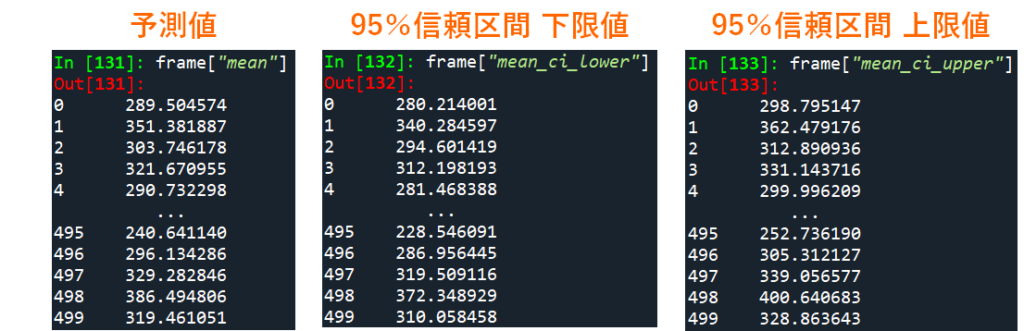
scikit learnライブラリで線形回帰分析
おまけに,scikit learnライブラリで線形回帰分析を実行する方法を紹介しておきます(公式).scikit learnライブラリはneural network系の手法も幅広く扱える非常に強力なライブラリではありますが,結果の表示方法などが少し初心者向けではないように思います.そのためこの記事ではおまけ的な扱いにしています.
どちらにせよ推定結果は同じですが,どうしてもscikit learnライブラリにこだわりたい!という方は,以下のコードを実行してもらえれば,上記のstatmodelsライブラリの結果と同じ回帰係数推定値などを得ることができます.
# scikit learnライブラリの線形回帰モデルを使える状態にする
from sklearn.linear_model import LinearRegression
# モデルの構築
ols = LinearRegression()
# 目的変数Yと説明変数X
Y = df[["outcome_num"]].values
X = df[["treat_num"]].values
# モデル推定
ols.fit(X,Y)
# 回帰係数を出力
ols.coef_まとめ
今回はPythonにおいて,statmodelsを利用した線形回帰分析の実行方法を紹介しました.線形回帰モデルは scikit learn パッケージなどでも実施可能ですが,statmodelsライブラリを使えばより簡単に結果のサマリーまで表示してくれるため,初心者にも非常におすすめです.
またRユーザーにとっても理解しやすい関数構造になっていると同時に,同時にscikit learnなどに慣れている人でも問題なく使えるように構築されています.
またPythonの実践的な使い方を体系的に学びたいという方は以下のスクールがおすすめです.以下の記事でこれらのスクールの比較も行っていますので,ぜひ参考にしてみてくださいね.






コメント